Soal fungsi komposisi invers merupakan topik menarik dalam matematika yang menggabungkan dua konsep penting: fungsi komposisi dan fungsi invers. Memahami keduanya sangat krusial karena memiliki aplikasi luas, mulai dari penyelesaian masalah matematika tingkat lanjut hingga penerapannya di berbagai bidang seperti ekonomi dan fisika. Artikel ini akan membahas secara detail konsep fungsi komposisi dan invers, menjelajahi cara mencari keduanya, serta mengaplikasikannya dalam berbagai contoh soal.
Kita akan memulai dengan definisi fungsi komposisi dan invers, kemudian mempelajari langkah-langkah mencari fungsi komposisi dan invers dari berbagai jenis fungsi, termasuk fungsi linear, kuadrat, dan eksponen. Selanjutnya, kita akan menelusuri sifat-sifat komposisi fungsi invers dan menyelesaikan berbagai contoh soal, termasuk soal cerita yang lebih menantang. Tujuannya adalah untuk memberikan pemahaman yang komprehensif dan kemampuan untuk menyelesaikan soal-soal fungsi komposisi invers dengan percaya diri.
Fungsi Komposisi dan Invers
Fungsi komposisi dan invers merupakan konsep penting dalam aljabar. Memahami keduanya sangat krusial dalam menyelesaikan berbagai permasalahan matematika, terutama yang berkaitan dengan relasi dan pemetaan. Artikel ini akan membahas pengertian dan sifat-sifat dari kedua konsep tersebut secara detail.
Definisi Fungsi Komposisi
Fungsi komposisi adalah penggabungan dua fungsi atau lebih menjadi satu fungsi baru. Jika kita memiliki fungsi f dan g, maka fungsi komposisi (f o g)(x) dibaca “f komposisi g” didefinisikan sebagai f(g(x)). Artinya, kita terlebih dahulu menghitung nilai g(x), kemudian hasil tersebut digunakan sebagai input untuk fungsi f.
Contoh: Misalkan f(x) = x² dan g(x) = x + 1. Maka (f o g)(x) = f(g(x)) = f(x + 1) = (x + 1)². Sebaliknya, (g o f)(x) = g(f(x)) = g(x²) = x² + 1. Perhatikan bahwa (f o g)(x) ≠ (g o f)(x) pada umumnya, menunjukkan bahwa komposisi fungsi tidak bersifat komutatif.
Ilustrasi Grafis Fungsi Komposisi
Bayangkan fungsi g memetakan titik x ke titik y, dan fungsi f memetakan titik y ke titik z. Fungsi komposisi (f o g) memetakan titik x langsung ke titik z melalui proses intermediet y. Secara visual, dapat diilustrasikan sebagai dua fungsi yang saling berurutan, di mana output dari fungsi pertama menjadi input dari fungsi kedua. Proses ini dapat digambarkan dengan diagram panah yang menunjukkan alur pemetaan dari x ke y dan kemudian dari y ke z.
Bentuk diagramnya bergantung pada jenis fungsi yang dikomposisikan (linear, kuadratik, dll), namun esensinya tetap sama: urutan pemetaan.
Definisi Fungsi Invers
Fungsi invers adalah fungsi yang membalikkan pemetaan suatu fungsi. Jika kita memiliki fungsi f yang memetakan x ke y, maka fungsi invers f⁻¹ memetakan y kembali ke x. Syarat utama suatu fungsi memiliki invers adalah fungsi tersebut harus bersifat bijektif (injektif dan surjektif), artinya setiap elemen dalam domain dipetakan ke tepat satu elemen dalam kodomain dan setiap elemen dalam kodomain memiliki pasangan dalam domain.
Contoh: Jika f(x) = 2x + 1, maka inversnya f⁻¹(x) dapat dicari dengan mengganti f(x) dengan y, lalu menyelesaikan persamaan untuk x dalam bentuk y. y = 2x + 1 berarti x = (y – 1)/2. Jadi, f⁻¹(x) = (x – 1)/2.
Ilustrasi Grafis Fungsi Invers
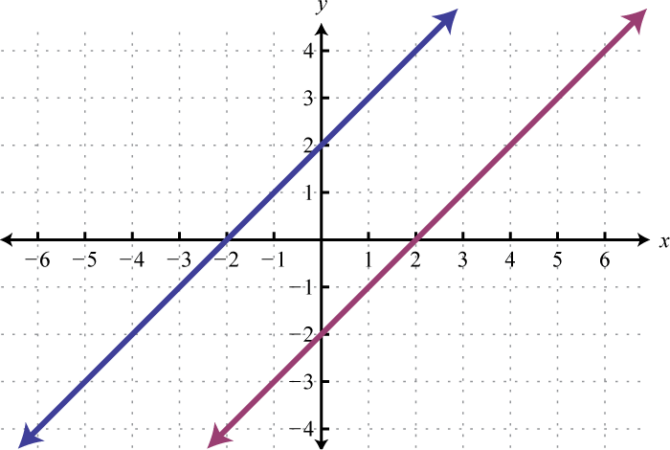
Secara grafis, grafik fungsi invers f⁻¹(x) merupakan pencerminan grafik fungsi f(x) terhadap garis y = x. Jika suatu titik (a, b) terletak pada grafik f(x), maka titik (b, a) akan terletak pada grafik f⁻¹(x). Ini menunjukkan relasi simetris antara fungsi dan inversnya terhadap garis y = x. Bentuk cerminan tersebut bergantung pada bentuk grafik fungsi asalnya.
Perbandingan Sifat Fungsi Komposisi dan Invers
| Sifat | Fungsi Komposisi | Fungsi Invers |
|---|---|---|
| Komutatif | Tidak selalu (f o g ≠ g o f) | Tidak berlaku (hanya berlaku untuk operasi invers itu sendiri) |
| Assosiatif | Ya ((f o g) o h = f o (g o h)) | Tidak berlaku (kecuali dalam konteks operasi invers) |
| Elemen identitas | Fungsi identitas (f o I = I o f = f) | f o f⁻¹ = f⁻¹ o f = I (fungsi identitas) |
| Syarat keberadaan | Tidak ada syarat khusus | Fungsi harus bijektif (injektif dan surjektif) |
Syarat Suatu Fungsi Memiliki Fungsi Invers
Suatu fungsi hanya memiliki fungsi invers jika fungsi tersebut bersifat bijektif. Bijektif berarti fungsi tersebut sekaligus injektif (satu-satu) dan surjektif (onto). Injektif berarti setiap elemen dalam domain dipetakan ke elemen yang berbeda dalam kodomain (tidak ada dua elemen domain yang dipetakan ke elemen kodomain yang sama). Surjektif berarti setiap elemen dalam kodomain memiliki pasangan dalam domain (semua elemen kodomain terpetakan).
Mencari Fungsi Komposisi
Fungsi komposisi merupakan operasi matematika yang menggabungkan dua atau lebih fungsi untuk menghasilkan fungsi baru. Memahami cara mencari fungsi komposisi sangat penting dalam berbagai aplikasi matematika, terutama dalam kalkulus dan aljabar. Pada bagian ini, kita akan mempelajari langkah-langkah untuk mencari fungsi komposisi dan beberapa contoh penerapannya pada fungsi linear dan kuadrat.
Langkah-langkah Mencari Fungsi Komposisi
Mencari fungsi komposisi, baik (f o g)(x) maupun (g o f)(x), melibatkan substitusi. Prosesnya relatif sederhana, namun ketelitian sangat dibutuhkan untuk menghindari kesalahan perhitungan.
- (f o g)(x): Substitusikan fungsi g(x) ke dalam fungsi f(x) di setiap tempat terdapat variabel x pada f(x). Hasilnya adalah fungsi komposisi (f o g)(x).
- (g o f)(x): Substitusikan fungsi f(x) ke dalam fungsi g(x) di setiap tempat terdapat variabel x pada g(x). Hasilnya adalah fungsi komposisi (g o f)(x).
Perlu diingat bahwa urutan operasi dalam fungsi komposisi sangat penting. (f o g)(x) berbeda dengan (g o f)(x), kecuali dalam kasus khusus di mana fungsi f dan g bersifat komutatif.
Contoh Fungsi Komposisi Dua Fungsi Linear
Misalkan f(x) = 2x + 1 dan g(x) = x – 3. Mari kita cari (f o g)(x) dan (g o f)(x).
- (f o g)(x) = f(g(x)) = f(x – 3) = 2(x – 3) + 1 = 2x – 6 + 1 = 2x – 5
- (g o f)(x) = g(f(x)) = g(2x + 1) = (2x + 1)
3 = 2x – 2
Dari contoh ini terlihat jelas bahwa (f o g)(x) ≠ (g o f)(x).
Contoh Fungsi Komposisi Dua Fungsi Kuadrat
Misalkan f(x) = x² + 2 dan g(x) = x²
-1. Kita akan mencari (f o g)(x) dan (g o f)(x).
- (f o g)(x) = f(g(x)) = f(x²
- 1) = (x²
- 1)² + 2 = x⁴
- 2x² + 1 + 2 = x⁴
- 2x² + 3
- (g o f)(x) = g(f(x)) = g(x² + 2) = (x² + 2)²
1 = x⁴ + 4x² + 4 – 1 = x⁴ + 4x² + 3
Sekali lagi, (f o g)(x) ≠ (g o f)(x) dalam kasus ini.
Contoh Fungsi Komposisi Fungsi Linear dan Fungsi Kuadrat
Misalkan f(x) = x² dan g(x) = 3x + 2. Mari kita cari (f o g)(x) dan (g o f)(x).
- (f o g)(x) = f(g(x)) = f(3x + 2) = (3x + 2)² = 9x² + 12x + 4
- (g o f)(x) = g(f(x)) = g(x²) = 3(x²) + 2 = 3x² + 2
Contoh ini kembali menunjukkan perbedaan antara (f o g)(x) dan (g o f)(x).
Mencari Fungsi Komposisi dengan Diagram Panah
Diagram panah dapat digunakan untuk memvisualisasikan proses komposisi fungsi. Misalkan kita memiliki fungsi f dan g yang dipetakan sebagai berikut:
Fungsi f: x → f(x) (misalnya, 1 → 3, 2 → 5, 3 → 7)
Fungsi g: x → g(x) (misalnya, 3 → 9, 5 → 11, 7 → 13)
Untuk mencari (g o f)(1), kita pertama-tama mengikuti panah dari 1 melalui fungsi f, yang menghasilkan 3. Kemudian, kita mengikuti panah dari 3 melalui fungsi g, yang menghasilkan 9. Jadi, (g o f)(1) = 9. Proses ini dapat diulangi untuk nilai x lainnya untuk membangun fungsi komposisi (g o f)(x) secara visual.
Diagram panah memberikan representasi grafis yang jelas tentang bagaimana nilai-nilai dipetakan melalui fungsi komposisi, membantu memahami proses substitusi secara visual.
Mencari Fungsi Invers

Mencari fungsi invers merupakan proses menemukan fungsi yang membalikkan pemetaan dari suatu fungsi. Jika kita memiliki fungsi f(x) yang memetakan x ke y, maka fungsi invers f⁻¹(x) akan memetakan y kembali ke x. Keberadaan fungsi invers bergantung pada sifat fungsi asal, yaitu fungsi harus bersifat bijektif (injektif dan surjektif). Proses pencarian fungsi invers melibatkan beberapa langkah sistematis yang akan dijelaskan berikut ini.
Secara umum, untuk menemukan fungsi invers, kita perlu melakukan manipulasi aljabar untuk menyatakan x sebagai fungsi dari y, kemudian kita tukar variabel x dan y.
Langkah-Langkah Mencari Fungsi Invers
Berikut langkah-langkah umum untuk mencari fungsi invers f⁻¹(x) dari suatu fungsi f(x):
- Tuliskan fungsi dalam bentuk y = f(x).
- Tukar variabel x dan y, sehingga persamaan menjadi x = f(y).
- Selesaikan persamaan x = f(y) untuk y, sehingga y dinyatakan sebagai fungsi dari x.
- Ganti y dengan notasi f⁻¹(x) untuk menyatakan fungsi invers.
Penting untuk diingat bahwa tidak semua fungsi memiliki invers. Fungsi harus bersifat bijektif agar inversnya ada.
Contoh Soal: Fungsi Invers Fungsi Linear, Soal fungsi komposisi invers
Misalkan kita memiliki fungsi linear f(x) = 2x +
3. Untuk mencari inversnya, ikuti langkah-langkah berikut:
- y = 2x + 3
- x = 2y + 3
- x – 3 = 2y
- y = (x – 3)/2
- f⁻¹(x) = (x – 3)/2
Jadi, fungsi invers dari f(x) = 2x + 3 adalah f⁻¹(x) = (x – 3)/2.
Contoh Soal: Fungsi Invers Fungsi Kuadrat
Fungsi kuadrat umumnya tidak memiliki invers pada seluruh domainnya karena tidak bijektif. Namun, jika kita membatasi domainnya, invers dapat ditemukan. Misalkan kita memiliki fungsi kuadrat f(x) = x² dengan domain x ≥
0. Langkah-langkah mencari inversnya:
- y = x²
- x = y²
- y = √x (karena domain x ≥ 0, kita hanya mengambil akar positif)
- f⁻¹(x) = √x
Jadi, fungsi invers dari f(x) = x² (dengan x ≥ 0) adalah f⁻¹(x) = √x.
Contoh Soal: Fungsi Invers Fungsi Eksponen
Misalkan kita memiliki fungsi eksponen f(x) = e x. Untuk mencari inversnya:
- y = ex
- x = e y
- y = ln(x)
- f⁻¹(x) = ln(x)
Jadi, fungsi invers dari f(x) = e x adalah f⁻¹(x) = ln(x).
Tabel Fungsi dan Fungsi Inversnya
Berikut tabel yang menunjukkan beberapa fungsi dan fungsi inversnya. Perlu diingat bahwa domain dan kodomain fungsi mempengaruhi keberadaan dan bentuk fungsi inversnya.
| Fungsi f(x) | Fungsi Invers f⁻¹(x) |
|---|---|
| x + 2 | x – 2 |
| 3x | x/3 |
| x² (x ≥ 0) | √x |
| ex | ln(x) |
| 2x | log₂(x) |
Komposisi Fungsi Invers
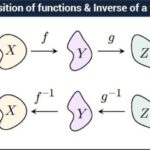
Fungsi invers, sebagai kebalikan dari suatu fungsi, memiliki sifat-sifat menarik ketika dikomposisikan dengan fungsi asalnya. Pemahaman komposisi fungsi invers sangat penting dalam menyelesaikan berbagai permasalahan matematika, khususnya dalam aljabar dan kalkulus. Komposisi fungsi invers menghasilkan identitas, suatu sifat yang memudahkan penyelesaian masalah yang kompleks.
Sifat-sifat Komposisi Fungsi Invers
Komposisi fungsi invers memiliki dua sifat utama yang perlu dipahami. Sifat-sifat ini berkaitan dengan hasil komposisi fungsi dengan inversnya, baik urutan fungsi maupun inversnya.
- (f o f⁻¹)(x) = x : Komposisi fungsi f dengan inversnya f⁻¹ menghasilkan x (variabel input).
- (f⁻¹ o f)(x) = x : Komposisi invers fungsi f dengan fungsi f sendiri juga menghasilkan x (variabel input).
Sifat-sifat ini menunjukkan bahwa komposisi fungsi dengan inversnya saling meniadakan efek satu sama lain, menghasilkan kembali variabel input asalnya.
Contoh Soal Pembuktian Sifat Komposisi Fungsi Invers
Misalkan fungsi f(x) = 2x +
3. Invers dari fungsi f(x), yaitu f⁻¹(x), dapat dicari dengan langkah-langkah sebagai berikut: y = 2x + 3, kemudian tukar x dan y menjadi x = 2y + 3. Selanjutnya, selesaikan persamaan tersebut untuk y, sehingga diperoleh y = (x – 3)/2. Maka f⁻¹(x) = (x – 3)/2.
Sekarang kita buktikan sifat (f o f⁻¹)(x) = x:
(f o f⁻¹)(x) = f(f⁻¹(x)) = f((x – 3)/2) = 2((x – 3)/2) + 3 = x – 3 + 3 = x
Selanjutnya, kita buktikan sifat (f⁻¹ o f)(x) = x:
(f⁻¹ o f)(x) = f⁻¹(f(x)) = f⁻¹(2x + 3) = ((2x + 3)
3)/2 = 2x/2 = x
Contoh ini membuktikan bahwa untuk fungsi f(x) = 2x + 3, komposisi fungsi dengan inversnya menghasilkan identitas, yaitu x.
Contoh Soal Pencarian Fungsi Invers dari Fungsi Komposisi
Diberikan fungsi komposisi (g o f)(x) = 2x + 4, dengan f(x) = x + 1. Tentukan fungsi invers dari (g o f)(x).
Langkah pertama adalah mencari fungsi g(x). Karena (g o f)(x) = g(f(x)) = 2x + 4 dan f(x) = x + 1, maka g(x + 1) = 2x + 4. Dengan mensubstitusikan u = x + 1 (maka x = u – 1), kita peroleh g(u) = 2(u – 1) + 4 = 2u + 2. Jadi, g(x) = 2x + 2.
Selanjutnya, kita cari invers dari (g o f)(x) = 2x +
4. Misalkan y = 2x +
4. Tukar x dan y menjadi x = 2y +
4. Selesaikan untuk y: y = (x – 4)/2. Jadi, invers dari (g o f)(x) adalah (x – 4)/2.
Contoh Soal Cerita yang Melibatkan Fungsi Komposisi dan Invers
Sebuah toko pakaian memberikan diskon 20% untuk semua barang, kemudian memberikan diskon tambahan 10% untuk barang yang sudah didiskon. Misalkan harga awal barang adalah x rupiah. Tentukan fungsi yang merepresentasikan harga akhir barang setelah diskon dan fungsi inversnya untuk menghitung harga awal barang jika harga akhir diketahui.
Fungsi diskon pertama: f(x) = x – 0.2x = 0.8x. Fungsi diskon kedua: g(x) = x – 0.1x = 0.9x. Fungsi komposisi yang merepresentasikan harga akhir adalah (g o f)(x) = g(f(x)) = g(0.8x) = 0.9(0.8x) = 0.72x.
Untuk mencari fungsi invers, misalkan y = 0.72x. Tukar x dan y menjadi x = 0.72y. Selesaikan untuk y: y = x/0.72. Jadi, fungsi inversnya adalah f⁻¹(x) = x/0.72. Fungsi ini dapat digunakan untuk menghitung harga awal barang jika harga akhir setelah diskon diketahui.
Langkah-langkah Menyelesaikan Soal yang Melibatkan Komposisi Fungsi Invers
- Identifikasi fungsi-fungsi yang terlibat dan tentukan invers dari fungsi-fungsi tersebut jika diperlukan.
- Lakukan komposisi fungsi sesuai dengan urutan yang diberikan dalam soal.
- Jika diperlukan, cari invers dari fungsi komposisi yang telah diperoleh dengan cara menukar variabel dependen dan independen, lalu menyelesaikan untuk variabel dependen.
- Selesaikan soal sesuai dengan konteks yang diberikan.
Penerapan Fungsi Komposisi dan Invers
Fungsi komposisi dan invers, meskipun mungkin tampak abstrak pada awalnya, memiliki penerapan yang luas dan signifikan dalam berbagai bidang kehidupan. Pemahaman mendalam tentang konsep ini memungkinkan kita untuk memodelkan dan menyelesaikan masalah kompleks dengan cara yang efisien dan sistematis. Berikut beberapa contoh penerapannya dalam kehidupan sehari-hari dan berbagai disiplin ilmu.
Penerapan dalam Kehidupan Sehari-hari
Fungsi komposisi dan invers seringkali bekerja di balik layar dalam aktivitas sehari-hari kita, tanpa kita sadari. Sebagai contoh, bayangkan proses memasak sebuah resep. Setiap langkah dalam resep (misalnya, mencampur bahan, memanggang, menambahkan bumbu) dapat dianggap sebagai fungsi. Fungsi komposisi terjadi ketika kita menggabungkan beberapa langkah ini untuk mencapai hasil akhir, yaitu hidangan yang matang. Sedangkan fungsi invers dapat dianalogikan dengan proses membalikkan langkah-langkah tersebut, misalnya, jika kita ingin mengetahui jumlah bahan awal dari hidangan yang sudah jadi.
Contoh lain adalah konversi satuan. Mengubah suhu dari Celcius ke Fahrenheit, atau sebaliknya, melibatkan fungsi komposisi dan invers. Rumus konversi itu sendiri merupakan fungsi, dan kita dapat menggunakan fungsi invers untuk mendapatkan nilai baliknya.
Penerapan dalam Bidang Ekonomi
Dalam ekonomi, fungsi komposisi dan invers digunakan untuk memodelkan hubungan antara berbagai variabel ekonomi. Misalnya, fungsi permintaan dapat dikomposisikan dengan fungsi penawaran untuk menentukan harga keseimbangan pasar. Berikut contoh soal:
Misalkan fungsi permintaan suatu barang adalah P = 100 – 2Q dan fungsi penawarannya adalah P = 20 + Q, dengan P adalah harga dan Q adalah kuantitas. Untuk mencari harga keseimbangan, kita perlu menyelesaikan persamaan 100 – 2Q = 20 + Q. Proses ini melibatkan konsep fungsi komposisi, di mana fungsi permintaan dan penawaran “dikomposisikan” untuk menemukan titik potongnya.
Selanjutnya, jika kita ingin mencari kuantitas yang diminta pada harga tertentu, kita dapat menggunakan fungsi invers dari fungsi permintaan.
Penerapan dalam Bidang Fisika
Dalam fisika, fungsi komposisi dan invers sering digunakan untuk menganalisis gerak benda. Misalnya, pergerakan proyektil yang dipengaruhi gravitasi dapat dimodelkan dengan menggunakan fungsi komposisi dari beberapa fungsi yang menggambarkan kecepatan horizontal dan vertikal. Berikut contoh soal:
Sebuah benda dilempar dengan kecepatan awal v 0 dan sudut elevasi θ. Posisi horizontal (x) dan vertikal (y) benda pada waktu t dapat dinyatakan sebagai fungsi dari waktu. Untuk mencari posisi benda pada waktu tertentu, kita dapat menggunakan fungsi komposisi dari fungsi x(t) dan y(t). Jika kita ingin mengetahui waktu yang dibutuhkan benda untuk mencapai ketinggian tertentu, kita dapat menggunakan fungsi invers dari fungsi y(t).
Pentingnya Memahami Fungsi Komposisi dan Invers dalam Matematika
Pemahaman yang mendalam tentang fungsi komposisi dan invers merupakan kunci untuk menguasai berbagai konsep matematika yang lebih lanjut. Konsep ini membentuk dasar bagi kalkulus, aljabar linear, dan banyak bidang matematika lainnya. Kemampuan untuk mengoperasikan dan memanipulasi fungsi-fungsi ini memungkinkan kita untuk memecahkan masalah yang kompleks dan mengembangkan model matematika yang akurat dan efisien.
Penerapan di Bidang Studi Lainnya
Konsep fungsi komposisi dan invers tidak hanya terbatas pada matematika, ekonomi, dan fisika. Konsep ini juga diterapkan secara luas dalam berbagai bidang studi lain, antara lain:
- Ilmu Komputer: Dalam ilmu komputer, fungsi komposisi digunakan dalam pemrograman fungsional dan dalam desain algoritma.
- Statistika: Fungsi invers digunakan dalam transformasi data dan dalam penentuan fungsi distribusi probabilitas.
- Rekayasa: Fungsi komposisi dan invers digunakan dalam pemodelan sistem dan dalam analisis sinyal.
- Biologi: Fungsi komposisi dan invers dapat digunakan untuk memodelkan pertumbuhan populasi dan reaksi biokimia.
Kesimpulan: Soal Fungsi Komposisi Invers
Setelah mempelajari konsep fungsi komposisi dan invers secara mendalam, kita dapat melihat betapa kuatnya kedua konsep ini dalam menyelesaikan berbagai permasalahan. Kemampuan untuk menemukan fungsi invers dan mengkomposisikan fungsi-fungsi merupakan keterampilan yang berharga, tidak hanya dalam matematika, tetapi juga dalam berbagai disiplin ilmu lainnya. Dengan pemahaman yang kokoh, anda akan mampu menghadapi soal-soal yang lebih kompleks dan mengaplikasikannya dalam situasi nyata dengan lebih efektif.