
- Pengantar Bentuk Akar
- Metode Penyederhanaan Bentuk Akar
- Penyederhanaan Bentuk Akar dengan Koefisien
-
Penyederhanaan Bentuk Akar yang Kompleks
- Penyederhanaan Bentuk Akar dengan Operasi Perkalian dan Pembagian
- Penyederhanaan Bentuk Akar yang Mengandung Variabel
- Penyederhanaan Bentuk Akar Pangkat Tiga atau Lebih Tinggi
- Contoh Soal Penyederhanaan Bentuk Akar Kompleks dan Penyelesaiannya
- Perbandingan Tingkat Kesulitan Penyederhanaan Bentuk Akar Sederhana dan Kompleks
-
Penerapan Penyederhanaan Bentuk Akar: Sederhanakanlah Bentuk Akar Berikut
- Contoh Penerapan Penyederhanaan Bentuk Akar dalam Pemecahan Masalah Matematika
- Pentingnya Penyederhanaan Bentuk Akar dalam Berbagai Konteks Matematika
- Contoh Soal Cerita yang Penyelesaiannya Memerlukan Penyederhanaan Bentuk Akar
- Ilustrasi Aplikasi Penyederhanaan Bentuk Akar dalam Geometri
- Penyederhanaan Bentuk Akar untuk Menyederhanakan Perhitungan
- Kesimpulan Akhir
Sederhanakanlah bentuk akar berikut: Pernahkah Anda merasa kesulitan menghadapi bentuk akar yang rumit dalam perhitungan matematika? Bentuk akar, meskipun tampak sederhana, dapat menjadi tantangan jika tidak dipahami dengan baik. Panduan ini akan membantu Anda menguasai teknik penyederhanaan bentuk akar, mulai dari yang paling dasar hingga yang kompleks, sehingga Anda dapat menyelesaikan soal matematika dengan lebih mudah dan efisien.
Kita akan menjelajahi berbagai metode penyederhanaan, termasuk faktorisasi prima dan penggunaan sifat-sifat akar. Dengan contoh-contoh soal dan langkah-langkah yang jelas, Anda akan mampu menyederhanakan bentuk akar yang mengandung koefisien, pecahan, variabel, dan bahkan akar pangkat tiga atau lebih tinggi. Mari kita mulai perjalanan untuk menguasai penyederhanaan bentuk akar!
Pengantar Bentuk Akar
Bentuk akar merupakan suatu cara penulisan bilangan irasional yang mengandung akar kuadrat, akar pangkat tiga, atau akar pangkat lainnya. Penyederhanaan bentuk akar bertujuan untuk menyajikan bilangan irasional tersebut dalam bentuk yang lebih sederhana dan mudah dipahami. Proses ini melibatkan pengurangan bilangan di dalam tanda akar dan menyederhanakannya sehingga tidak ada lagi faktor kuadrat sempurna di dalam akar.
Pemahaman tentang bentuk akar dan penyederhanaannya penting dalam berbagai bidang matematika, khususnya aljabar dan kalkulus. Kemampuan untuk menyederhanakan bentuk akar memungkinkan perhitungan yang lebih efisien dan hasil yang lebih akurat.
Contoh Bentuk Akar Sederhana dan Kompleks
Bentuk akar sederhana umumnya hanya melibatkan satu bilangan bulat di dalam tanda akar, misalnya √4, √9, atau √16. Sedangkan bentuk akar kompleks melibatkan bilangan yang lebih besar, perkalian, atau kombinasi bilangan dan variabel di dalam tanda akar, contohnya √12, √75, atau √(2x²y).
- √4 = 2 (sederhana)
- √12 = 2√3 (kompleks, sudah disederhanakan)
- √75 = 5√3 (kompleks, sudah disederhanakan)
- √(x²y) = x√y (kompleks, sudah disederhanakan, dengan asumsi x≥0)
Perbedaan Bentuk Akar Sederhana dan Bentuk Akar yang Sudah Disederhanakan
Perbedaan utama terletak pada keberadaan faktor kuadrat sempurna di dalam tanda akar. Bentuk akar sederhana mungkin masih mengandung faktor kuadrat sempurna yang dapat dikeluarkan, sedangkan bentuk akar yang sudah disederhanakan tidak lagi mengandung faktor kuadrat sempurna di dalam akar. Bentuk akar yang sudah disederhanakan lebih efisien dan mudah untuk dioperasikan dalam perhitungan selanjutnya.
Tabel Perbandingan Bentuk Akar Sebelum dan Sesudah Penyederhanaan
| Bentuk Akar Awal | Faktorisasi | Penyederhanaan | Bentuk Akar Sederhana |
|---|---|---|---|
| √12 | 2 x 2 x 3 | √(2² x 3) = 2√3 | 2√3 |
| √75 | 5 x 5 x 3 | √(5² x 3) = 5√3 | 5√3 |
| √18 | 2 x 3 x 3 | √(3² x 2) = 3√2 | 3√2 |
| √20 | 2 x 2 x 5 | √(2² x 5) = 2√5 | 2√5 |
Ilustrasi Penyederhanaan Bentuk Akar
Misalnya, untuk menyederhanakan √12, kita dapat memfaktorkan 12 menjadi 4 x
3. Karena 4 adalah kuadrat sempurna (2²), kita dapat mengeluarkannya dari tanda akar. Prosesnya dapat divisualisasikan sebagai berikut: Bayangkan persegi dengan luas 12 satuan. Kita dapat membagi persegi ini menjadi dua persegi kecil dengan luas 4 satuan (2×2) dan satu persegi panjang dengan luas 3 satuan.
Luas persegi dengan sisi 2 satuan adalah 4, jadi kita dapat mengambil 2 keluar dari akar, menyisakan √3 di dalam. Jadi, √12 disederhanakan menjadi 2√3.
Metode Penyederhanaan Bentuk Akar
Penyederhanaan bentuk akar merupakan proses untuk mengubah bentuk akar menjadi bentuk yang lebih sederhana dan mudah dipahami. Proses ini penting dalam berbagai bidang matematika, terutama aljabar dan kalkulus. Dengan menyederhanakan bentuk akar, kita dapat melakukan operasi matematika dengan lebih efisien dan akurat.
Langkah-langkah Umum Penyederhanaan Bentuk Akar
Secara umum, menyederhanakan bentuk akar melibatkan beberapa langkah kunci. Proses ini bertujuan untuk mengeluarkan faktor-faktor sempurna dari dalam tanda akar. Dengan demikian, bentuk akar yang dihasilkan akan lebih ringkas dan mudah diinterpretasi.
- Cari faktor prima dari bilangan yang berada di dalam tanda akar.
- Kelompokkan faktor-faktor prima yang membentuk bilangan kuadrat sempurna.
- Keluarkan bilangan kuadrat sempurna dari dalam tanda akar sebagai akar kuadratnya.
- Sederhanakan bentuk akar yang tersisa.
Metode Faktorisasi Prima dalam Penyederhanaan Bentuk Akar
Faktorisasi prima merupakan teknik yang efektif untuk menyederhanakan bentuk akar. Dengan memecah bilangan di dalam tanda akar menjadi faktor-faktor prima, kita dapat dengan mudah mengidentifikasi bilangan kuadrat sempurna yang dapat dikeluarkan.
Contoh: Sederhanakan √72. Faktorisasi prima dari 72 adalah 2³ x 3². Maka √72 = √(2² x 2 x 3²) = √(2² x 3²) x √2 = 2 x 3 x √2 = 6√2.
Penyederhanaan Bentuk Akar dengan Menggunakan Sifat-sifat Akar
Sifat-sifat akar, seperti √(a x b) = √a x √b dan √(a/b) = √a / √b, juga dapat digunakan untuk menyederhanakan bentuk akar. Penerapan sifat-sifat ini memungkinkan kita untuk memanipulasi bentuk akar dan mengeluarkan faktor-faktor yang memungkinkan.
Contoh: Sederhanakan √(27/4). Menggunakan sifat √(a/b) = √a / √b, kita peroleh √(27/4) = √27 / √4 = (√9 x √3) / 2 = (3√3) / 2.
Contoh Penyederhanaan Bentuk Akar dengan Metode yang Berbeda
Berikut contoh penyederhanaan bentuk akar dengan berbagai metode:
Contoh 1 (Metode Faktorisasi Prima): Sederhanakan √128. Faktorisasi prima dari 128 adalah 27 = 2 6 x 2. Maka √128 = √(2 6 x 2) = 2 3√2 = 8√2.
Contoh 2 (Menggunakan Sifat Akar): Sederhanakan √(48 x 3). Dengan menggunakan sifat √(a x b) = √a x √b, kita peroleh √(48 x 3) = √144 = 12.
Penyederhanaan Bentuk Akar dengan Koefisien
Penyederhanaan bentuk akar dengan koefisien merupakan keterampilan penting dalam aljabar. Memahami cara menyederhanakan bentuk akar ini akan membantu dalam menyelesaikan berbagai persamaan dan soal matematika yang lebih kompleks. Proses ini melibatkan penggabungan konsep perkalian akar dan faktorisasi bilangan.
Pada dasarnya, menyederhanakan bentuk akar dengan koefisien berarti kita mencari bentuk paling sederhana dari suatu bentuk akar yang memiliki angka di depan (koefisien) dan di dalam tanda akar. Tujuannya adalah untuk mendapatkan bentuk akar yang lebih ringkas dan mudah dipahami.
Contoh Penyederhanaan Bentuk Akar dengan Koefisien
Misalnya, kita ingin menyederhanakan bentuk akar 6√72. Langkah pertama adalah memfaktorkan angka di dalam akar (72) menjadi faktor-faktor prima. 72 = 2 x 2 x 2 x 3 x 3 = 2 3 x 3 2. Kemudian, kita keluarkan faktor-faktor yang memiliki pangkat genap dari dalam akar. Karena 2 2 dan 3 2 memiliki pangkat genap, kita dapat mengeluarkannya dari dalam akar sebagai 2 dan 3.
Hasilnya adalah 6 x 2 x 3 √(2) = 36√2.
Penyederhanaan Bentuk Akar dengan Koefisien yang Melibatkan Operasi Penjumlahan dan Pengurangan
Ketika menghadapi bentuk akar dengan koefisien yang melibatkan penjumlahan atau pengurangan, kita perlu memastikan bahwa bentuk akarnya sama sebelum melakukan operasi. Sebagai contoh, perhatikan 2√2 + 3√8 – √
18. Kita sederhanakan terlebih dahulu setiap bentuk akar: √8 = √(4 x 2) = 2√2 dan √18 = √(9 x 2) = 3√2. Maka persamaan menjadi 2√2 + 3(2√2)
-3√2 = 2√2 + 6√2 – 3√2 = 5√2.
Langkah-langkah Penyederhanaan Bentuk Akar dengan Koefisien, Sederhanakanlah bentuk akar berikut
- Faktorkan angka di dalam akar menjadi faktor-faktor prima.
- Keluarkan faktor-faktor yang memiliki pangkat genap dari dalam akar.
- Kalikan koefisien dengan angka yang telah dikeluarkan dari dalam akar.
- Sederhanakan hasil perkalian.
- Jika terdapat operasi penjumlahan atau pengurangan, pastikan bentuk akarnya sama sebelum melakukan operasi.
Contoh Soal Bentuk Akar dengan Koefisien dan Pecahan
Perhatikan soal berikut: Sederhanakan (1/2)√48 + 2√(3/4). Pertama, sederhanakan bentuk akarnya: √48 = √(16 x 3) = 4√3 dan √(3/4) = √3/2. Maka persamaan menjadi (1/2)(4√3) + 2(√3/2) = 2√3 + √3 = 3√3.
Penyederhanaan Bentuk Akar yang Kompleks
Setelah memahami penyederhanaan bentuk akar sederhana, mari kita lanjutkan dengan bentuk akar yang lebih kompleks. Penyederhanaan ini melibatkan operasi perkalian, pembagian, dan bahkan akar pangkat tiga atau lebih tinggi, serta melibatkan variabel. Pemahaman yang baik tentang konsep ini akan sangat membantu dalam menyelesaikan berbagai permasalahan matematika, khususnya dalam aljabar.
Penyederhanaan Bentuk Akar dengan Operasi Perkalian dan Pembagian
Menyederhanakan bentuk akar yang melibatkan perkalian dan pembagian didasarkan pada sifat-sifat akar. Pada perkalian, akar dari perkalian dua bilangan sama dengan perkalian akar masing-masing bilangan. Sebaliknya, pada pembagian, akar dari pembagian dua bilangan sama dengan pembagian akar masing-masing bilangan. Dengan memahami sifat ini, kita dapat menyederhanakan bentuk akar yang kompleks menjadi bentuk yang lebih sederhana dan mudah dipahami.
Sebagai contoh, √12 x √3 = √(12 x 3) = √36 = 6. Sedangkan untuk pembagian, misalnya √16 / √4 = √(16/4) = √4 = 2.
Penyederhanaan Bentuk Akar yang Mengandung Variabel
Penyederhanaan bentuk akar yang mengandung variabel mengikuti prinsip yang sama seperti penyederhanaan bentuk akar tanpa variabel. Perbedaannya terletak pada penanganan variabel tersebut. Kita perlu memisahkan variabel dan konstanta sebelum menyederhanakan akar. Misalnya, √(4x²y) dapat disederhanakan menjadi 2|x|√y, dengan catatan x dan y adalah bilangan real non-negatif. Nilai mutlak pada x diperlukan karena akar kuadrat selalu menghasilkan nilai non-negatif.
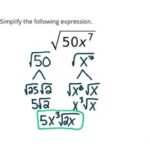
Penyederhanaan Bentuk Akar Pangkat Tiga atau Lebih Tinggi
Penyederhanaan bentuk akar pangkat tiga atau lebih tinggi juga didasarkan pada prinsip yang serupa. Kita perlu mencari faktor-faktor yang merupakan pangkat sempurna dari indeks akar. Misalnya, untuk menyederhanakan ³√24, kita dapat mencari faktor dari 24 yang merupakan pangkat tiga sempurna. Karena 24 = 8 x 3, dan 8 = 2³, maka ³√24 = ³√(8 x 3) = ³√8 x ³√3 = 2³√3.
Contoh Soal Penyederhanaan Bentuk Akar Kompleks dan Penyelesaiannya
Mari kita selesaikan soal berikut: Sederhanakan √(75x⁴y³/12x²y).
- Pisahkan konstanta dan variabel: √(75/12) x √(x⁴/x²) x √(y³/y)
- Sederhanakan pecahan: √(25/4) x √x² x √y²
- Sederhanakan akar: (5/2)x|y|
Jadi, penyederhanaan dari √(75x⁴y³/12x²y) adalah (5/2)x|y| dengan catatan x dan y adalah bilangan real non-negatif.
Perbandingan Tingkat Kesulitan Penyederhanaan Bentuk Akar Sederhana dan Kompleks
| Aspek | Bentuk Akar Sederhana | Bentuk Akar Kompleks |
|---|---|---|
| Operasi | Hanya melibatkan akar kuadrat | Melibatkan perkalian, pembagian, akar pangkat tiga atau lebih tinggi |
| Variabel | Tanpa variabel atau variabel sederhana | Mengandung variabel dengan pangkat yang beragam |
| Tingkat Kesulitan | Relatif mudah | Lebih kompleks dan membutuhkan pemahaman yang lebih mendalam tentang sifat-sifat akar dan aljabar |
Penerapan Penyederhanaan Bentuk Akar: Sederhanakanlah Bentuk Akar Berikut
Penyederhanaan bentuk akar merupakan keterampilan dasar dalam matematika yang memiliki aplikasi luas dalam berbagai bidang. Kemampuan untuk menyederhanakan bentuk akar memungkinkan perhitungan yang lebih efisien dan pemahaman yang lebih baik terhadap konsep-konsep matematika yang lebih kompleks. Berikut beberapa penerapan penyederhanaan bentuk akar dalam pemecahan masalah.
Contoh Penerapan Penyederhanaan Bentuk Akar dalam Pemecahan Masalah Matematika
Misalnya, dalam menyelesaikan persamaan kuadrat, seringkali kita mendapatkan akar-akar yang berbentuk akar tidak rasional. Penyederhanaan bentuk akar memungkinkan kita untuk menyatakan akar-akar tersebut dalam bentuk yang lebih sederhana dan mudah dipahami. Sebagai contoh, jika kita memiliki akar √12, kita dapat menyederhanakannya menjadi 2√3. Bentuk sederhana ini memudahkan dalam perhitungan selanjutnya, seperti penjumlahan atau perkalian dengan akar lainnya.
Pentingnya Penyederhanaan Bentuk Akar dalam Berbagai Konteks Matematika
Penyederhanaan bentuk akar penting karena meningkatkan akurasi dan efisiensi perhitungan. Dalam geometri, misalnya, bentuk akar sering muncul saat menghitung panjang diagonal atau luas bangun datar. Bentuk akar yang sederhana memudahkan dalam perhitungan lebih lanjut dan interpretasi hasil. Selain itu, penyederhanaan bentuk akar juga krusial dalam kalkulus, aljabar, dan trigonometri.
Contoh Soal Cerita yang Penyelesaiannya Memerlukan Penyederhanaan Bentuk Akar
Sebuah tangga sepanjang 10 meter disandarkan pada dinding. Jarak kaki tangga dari dinding adalah 6 meter. Berapakah tinggi dinding yang dicapai oleh tangga tersebut? Penyelesaian soal ini memerlukan teorema Pythagoras, yang menghasilkan bentuk akar. Dengan menyederhanakan bentuk akar, kita dapat menentukan tinggi dinding dengan lebih akurat.
Penyelesaian: Menggunakan teorema Pythagoras, tinggi dinding (h) dapat dihitung dengan rumus: h² + 6² = 10². Maka h² = 100 – 36 = 64, sehingga h = √64 = 8 meter.
Ilustrasi Aplikasi Penyederhanaan Bentuk Akar dalam Geometri
Perhatikan segitiga siku-siku dengan panjang sisi siku-sikunya 1 dan 2. Panjang sisi miringnya adalah √(1² + 2²) = √5. Jika kita ingin menghitung luas segitiga tersebut, kita perlu mengalikan setengah dari hasil kali kedua sisi siku-siku, yaitu ½
– 1
– 2 = 1. Namun, jika kita ingin menghitung kelilingnya, kita perlu menambahkan panjang ketiga sisi, yaitu 1 + 2 + √5.
Dalam kasus ini, penyederhanaan bentuk akar √5 tidak mungkin dilakukan lebih lanjut, tetapi tetap penting untuk menyatakan keliling segitiga dengan tepat.
Penyederhanaan Bentuk Akar untuk Menyederhanakan Perhitungan
Penyederhanaan bentuk akar memungkinkan perhitungan yang lebih ringkas dan efisien. Misalnya, √72 dapat disederhanakan menjadi 6√2. Bentuk 6√2 lebih mudah dioperasikan dalam perhitungan selanjutnya dibandingkan dengan √72, terutama jika melibatkan operasi penjumlahan, pengurangan, perkalian, atau pembagian dengan akar lainnya. Hal ini menghindari perhitungan yang rumit dan mengurangi kemungkinan kesalahan.
Kesimpulan Akhir

Dengan memahami metode dan langkah-langkah penyederhanaan bentuk akar yang telah diuraikan, Anda kini memiliki bekal yang cukup untuk menghadapi berbagai bentuk soal yang melibatkan akar. Kemampuan menyederhanakan bentuk akar tidak hanya meningkatkan efisiensi perhitungan, tetapi juga membantu dalam memahami konsep matematika yang lebih kompleks. Teruslah berlatih dan jangan ragu untuk mengeksplorasi lebih dalam dunia matematika yang menarik ini.






