
Contoh soal program linear merupakan pintu gerbang untuk memahami teknik optimasi dalam berbagai bidang. Program linear, metode matematis untuk menemukan solusi terbaik dari suatu permasalahan dengan batasan tertentu, memiliki aplikasi luas mulai dari manajemen produksi hingga perencanaan keuangan. Artikel ini akan membahas secara detail konsep program linear, metode penyelesaiannya, serta berbagai contoh soal yang akan memperkuat pemahaman Anda.
Dari definisi program linear hingga aplikasi praktisnya, kita akan menjelajahi berbagai aspek penting. Dengan contoh soal yang beragam, mulai dari yang sederhana hingga yang kompleks, Anda akan mampu menguasai teknik penyelesaian program linear baik menggunakan metode grafik maupun metode Simplex. Siap untuk mengoptimalkan potensi Anda dalam pemecahan masalah?
Pengertian Program Linear
Program linear merupakan metode matematis yang digunakan untuk menemukan solusi optimal (nilai maksimum atau minimum) dari suatu fungsi objektif, dengan adanya kendala-kendala berupa persamaan atau pertidaksamaan linear. Metode ini sangat berguna dalam pengambilan keputusan di berbagai bidang, karena membantu dalam mengalokasikan sumber daya secara efisien untuk mencapai tujuan yang diinginkan. Dengan kata lain, program linear membantu kita menentukan cara terbaik untuk melakukan sesuatu, dengan mempertimbangkan keterbatasan yang ada.
Program linear membantu kita menyelesaikan masalah optimasi dengan cara yang sistematis dan terstruktur. Dengan merumuskan masalah dalam bentuk model matematika, kita dapat menganalisis berbagai kemungkinan solusi dan memilih yang paling optimal. Keunggulan utama program linear terletak pada kemampuannya untuk menangani masalah dengan banyak variabel dan kendala secara simultan, yang sulit dipecahkan hanya dengan intuisi atau perhitungan manual.
Contoh Penerapan Program Linear dalam Kehidupan Sehari-hari
Salah satu contoh penerapan program linear adalah dalam perencanaan produksi di sebuah pabrik. Misalnya, sebuah pabrik memproduksi dua jenis produk, A dan B, dengan masing-masing membutuhkan sumber daya berupa bahan baku dan waktu produksi yang berbeda. Pabrik ingin memaksimalkan keuntungannya dengan menentukan jumlah produk A dan B yang harus diproduksi, mengingat keterbatasan jumlah bahan baku dan waktu produksi yang tersedia.
Dengan menggunakan program linear, pabrik dapat menentukan kombinasi produksi yang optimal untuk mencapai keuntungan maksimum. Contoh lainnya adalah dalam penentuan alokasi anggaran pemasaran, optimasi portofolio investasi, atau bahkan dalam perencanaan menu makanan yang seimbang dan bergizi dengan anggaran terbatas.
Unsur-unsur Penting dalam Permasalahan Program Linear
Terdapat tiga unsur penting dalam permasalahan program linear:
- Variabel Keputusan: Variabel ini merepresentasikan kuantitas yang ingin kita tentukan nilainya untuk mencapai solusi optimal. Dalam contoh pabrik di atas, variabel keputusan adalah jumlah produk A dan B yang diproduksi.
- Fungsi Objektif: Fungsi ini menyatakan tujuan yang ingin dicapai, yang biasanya berupa memaksimalkan keuntungan atau meminimalkan biaya. Dalam contoh pabrik, fungsi objektif adalah memaksimalkan keuntungan total dari penjualan produk A dan B.
- Kendala: Kendala ini berupa persamaan atau pertidaksamaan linear yang membatasi nilai variabel keputusan. Dalam contoh pabrik, kendala berupa keterbatasan jumlah bahan baku dan waktu produksi yang tersedia.
Perbandingan Program Linear dengan Metode Optimasi Lainnya
Berikut tabel perbandingan program linear dengan metode optimasi lainnya:
| Metode | Keunggulan | Kelemahan | Contoh Penerapan |
|---|---|---|---|
| Program Linear | Dapat menangani banyak variabel dan kendala; solusi optimal terjamin; metode sistematis dan terstruktur. | Membutuhkan model matematis yang akurat; asumsi linearitas mungkin tidak selalu berlaku di dunia nyata. | Perencanaan produksi, alokasi sumber daya, penentuan portofolio investasi. |
| Metode Grafik | Mudah dipahami dan divisualisasikan, terutama untuk masalah dengan dua variabel. | Tidak efisien untuk masalah dengan lebih dari dua variabel; solusi hanya berupa pendekatan jika titik optimal tidak tepat berada pada titik potong garis kendala. | Perencanaan produksi sederhana dengan dua jenis produk; optimasi penggunaan lahan pertanian dengan dua jenis tanaman. |
Langkah-langkah Umum dalam Menyelesaikan Masalah Program Linear
Secara umum, langkah-langkah dalam menyelesaikan masalah program linear adalah sebagai berikut:
- Merumuskan Masalah: Tentukan variabel keputusan, fungsi objektif, dan kendala dalam bentuk matematis.
- Membuat Model Matematika: Tuliskan fungsi objektif dan kendala dalam bentuk persamaan atau pertidaksamaan linear.
- Menyelesaikan Model: Gunakan metode Simpleks atau metode grafik untuk mencari solusi optimal.
- Menganalisis Solusi: Interpretasikan solusi optimal dalam konteks masalah nyata.
Metode Penyelesaian Program Linear
Program linear, sebagai metode optimasi matematis, dapat diselesaikan melalui berbagai pendekatan. Dua metode yang umum digunakan adalah metode grafik dan metode Simplex. Metode grafik cocok untuk masalah dengan dua variabel, sementara metode Simplex lebih fleksibel dan dapat menangani masalah dengan banyak variabel. Pemilihan metode bergantung pada kompleksitas masalah dan jumlah variabel yang terlibat.
Penyelesaian Program Linear dengan Metode Grafik
Metode grafik memberikan representasi visual dari kendala dan fungsi objektif. Dengan memplot kendala pada bidang kartesius, kita dapat menentukan daerah yang memenuhi semua kendala (daerah feasible). Titik optimum, yang memaksimalkan atau meminimalkan fungsi objektif, terletak pada salah satu titik pojok daerah feasible.
Sebagai contoh, perhatikan masalah berikut: Sebuah perusahaan memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam mesin X dan 1 jam mesin Y, sedangkan produk B membutuhkan 1 jam mesin X dan 3 jam mesin Y. Tersedia 10 jam waktu mesin X dan 12 jam waktu mesin Y. Keuntungan per unit produk A adalah Rp 50.000 dan per unit produk B adalah Rp 70.000.
Berapa banyak unit produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan?
Kendala-kendalanya dapat dirumuskan sebagai berikut:
- 2A + B ≤ 10 (Kendala Mesin X)
- A + 3B ≤ 12 (Kendala Mesin Y)
- A ≥ 0
- B ≥ 0
Fungsi objektifnya adalah: Maksimumkan Z = 50.000A + 70.000B
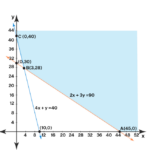
Dengan memplot kendala-kendala tersebut pada bidang kartesius, kita akan mendapatkan daerah feasible yang dibatasi oleh garis-garis 2A + B = 10, A + 3B = 12, A = 0, dan B = 0. Titik pojok daerah feasible kemudian diuji pada fungsi objektif untuk menentukan titik optimum yang memberikan keuntungan maksimum. Misalnya, titik pojok (2, 4) akan menghasilkan keuntungan sebesar Rp 380.000.
Setelah mengevaluasi semua titik pojok, titik optimum yang memberikan keuntungan maksimum dapat ditentukan. Gambar yang dihasilkan akan menampilkan daerah feasible yang diarsir, garis-garis kendala, dan titik-titik pojoknya, termasuk titik optimum yang memberikan keuntungan maksimum. Setiap garis kendala merepresentasikan satu persamaan kendala, dan titik-titik pojok merupakan titik potong antara dua atau lebih garis kendala.
Metode Simplex
Metode Simplex merupakan metode aljabar iteratif untuk menyelesaikan program linear. Metode ini lebih efisien daripada metode grafik, terutama untuk masalah dengan banyak variabel. Metode ini melibatkan pembentukan tabel Simplex, yang kemudian diiterasi hingga ditemukan solusi optimum.
Sebagai contoh, perhatikan masalah program linear yang berbeda: Sebuah pabrik memproduksi dua jenis barang, X dan Y. Barang X membutuhkan 2 unit bahan baku A dan 1 unit bahan baku B, sedangkan barang Y membutuhkan 1 unit bahan baku A dan 3 unit bahan baku B. Tersedia 10 unit bahan baku A dan 12 unit bahan baku B.
Keuntungan per unit barang X adalah Rp 60.000 dan per unit barang Y adalah Rp 80.000. Berapa banyak unit barang X dan Y yang harus diproduksi untuk memaksimalkan keuntungan?
Masalah ini dapat diformulasikan sebagai program linear dan diselesaikan menggunakan metode Simplex. Proses ini melibatkan beberapa iterasi, dengan setiap iterasi melibatkan pemilihan variabel masuk dan keluar, perhitungan rasio, dan pembaruan tabel Simplex. Setiap iterasi akan mendekati solusi optimum secara bertahap. Detail perhitungan setiap iterasi, termasuk pemilihan variabel, perhitungan rasio minimum, dan pembaruan nilai-nilai dalam tabel Simplex, akan dijelaskan secara rinci dalam langkah-langkah penyelesaian.
Perbandingan Metode Grafik dan Simplex
Metode grafik mudah dipahami dan divisualisasikan, tetapi hanya efektif untuk masalah dengan dua variabel. Metode Simplex lebih kompleks, tetapi dapat menangani masalah dengan banyak variabel. Efisiensi metode Simplex jauh lebih tinggi daripada metode grafik untuk masalah dengan lebih dari dua variabel. Kompleksitas perhitungan metode Simplex meningkat seiring dengan bertambahnya jumlah variabel, namun tetap lebih efisien daripada metode grafik untuk masalah berskala besar.
Contoh Soal Program Linear Berbagai Jenis

Program linear merupakan metode matematis yang digunakan untuk menyelesaikan masalah optimasi dengan kendala berupa persamaan atau pertidaksamaan linear. Pemahaman yang baik tentang program linear memerlukan latihan dengan berbagai variasi soal. Berikut ini beberapa contoh soal program linear yang meliputi berbagai jenis kendala dan fungsi objektif.
Contoh-contoh soal di bawah ini akan membantu Anda memahami penerapan program linear dalam berbagai skenario, mulai dari masalah sederhana hingga yang lebih kompleks melibatkan lebih dari dua variabel.
Contoh Soal Program Linear dengan Tiga Variabel
Sebuah perusahaan memproduksi tiga jenis produk: A, B, dan C. Setiap produk membutuhkan waktu produksi yang berbeda di tiga mesin yang tersedia. Produk A membutuhkan 2 jam di mesin 1, 1 jam di mesin 2, dan 3 jam di mesin 3. Produk B membutuhkan 1 jam di mesin 1, 3 jam di mesin 2, dan 2 jam di mesin 3.
Produk C membutuhkan 3 jam di mesin 1, 2 jam di mesin 2, dan 1 jam di mesin 3. Waktu operasional masing-masing mesin adalah 10 jam, 12 jam, dan 15 jam. Keuntungan dari setiap produk A, B, dan C berturut-turut adalah Rp 50.000, Rp 60.000, dan Rp 70.000. Berapa banyak masing-masing produk yang harus diproduksi untuk memaksimalkan keuntungan?
Soal ini melibatkan tiga variabel (jumlah produk A, B, dan C) dan tiga kendala (waktu operasional masing-masing mesin). Model matematika yang dapat disusun akan terdiri dari fungsi objektif (memaksimalkan keuntungan) dan sistem pertidaksamaan linear yang merepresentasikan kendala waktu produksi.
Contoh Soal Program Linear dengan Kendala Pertidaksamaan
Sebuah pabrik roti memproduksi dua jenis roti: roti tawar dan roti manis. Produksi roti tawar membutuhkan 2 kg tepung dan 1 kg gula per unit, sedangkan roti manis membutuhkan 1 kg tepung dan 2 kg gula per unit. Pabrik memiliki persediaan 10 kg tepung dan 8 kg gula. Keuntungan dari setiap unit roti tawar adalah Rp 10.000 dan roti manis Rp 15.000.
Berapa banyak roti tawar dan roti manis yang harus diproduksi untuk memaksimalkan keuntungan?
Kendala dalam soal ini berupa pertidaksamaan linear yang merepresentasikan keterbatasan bahan baku (tepung dan gula). Model matematika akan melibatkan dua variabel (jumlah roti tawar dan roti manis) dan dua pertidaksamaan linear sebagai kendala.
Contoh Soal Program Linear dengan Kendala Persamaan
Sebuah perusahaan memiliki dua jenis mesin, X dan Y, untuk memproduksi dua jenis produk, A dan B. Mesin X menghasilkan 2 unit produk A dan 1 unit produk B per jam, sedangkan mesin Y menghasilkan 1 unit produk A dan 2 unit produk B per jam. Perusahaan harus memproduksi tepat 10 unit produk A dan 12 unit produk B.
Biaya operasional mesin X adalah Rp 50.000 per jam dan mesin Y Rp 60.000 per jam. Berapa jam masing-masing mesin harus dioperasikan untuk meminimalkan biaya?
Soal ini unik karena kendalanya berupa persamaan linear, yang mencerminkan kebutuhan produksi yang tepat. Fungsi objektifnya adalah meminimalkan biaya operasional.
Contoh Soal Program Linear dengan Fungsi Objektif Maksimisasi
Sebuah perusahaan memproduksi dua jenis produk, X dan Y. Setiap unit produk X membutuhkan 2 jam kerja dan 1 kg bahan baku, sedangkan setiap unit produk Y membutuhkan 1 jam kerja dan 2 kg bahan baku. Tersedia 100 jam kerja dan 80 kg bahan baku. Keuntungan dari setiap unit produk X adalah Rp 20.000 dan produk Y Rp 30.000.
Berapa banyak produk X dan Y yang harus diproduksi untuk memaksimalkan keuntungan?
Soal ini merupakan contoh klasik program linear dengan fungsi objektif maksimisasi (memaksimalkan keuntungan) dan kendala berupa keterbatasan sumber daya (waktu kerja dan bahan baku).
Contoh Soal Program Linear dengan Fungsi Objektif Minimisasi
Sebuah perusahaan memiliki dua gudang, A dan B, yang menyimpan bahan baku. Gudang A memiliki 100 unit bahan baku dan gudang B memiliki 80 unit. Perusahaan harus mengirimkan bahan baku ke dua pabrik, X dan Y. Pabrik X membutuhkan 50 unit bahan baku dan pabrik Y membutuhkan 70 unit. Biaya pengiriman dari gudang A ke pabrik X adalah Rp 1.000 per unit, dari gudang A ke pabrik Y adalah Rp 1.500 per unit, dari gudang B ke pabrik X adalah Rp 1.200 per unit, dan dari gudang B ke pabrik Y adalah Rp 1.000 per unit.
Berapa banyak bahan baku yang harus dikirim dari masing-masing gudang ke masing-masing pabrik untuk meminimalkan biaya pengiriman?
Soal ini menunjukkan contoh program linear dengan fungsi objektif minimisasi (meminimalkan biaya pengiriman). Kendala dalam soal ini adalah ketersediaan bahan baku di masing-masing gudang dan kebutuhan bahan baku di masing-masing pabrik.
Interpretasi Hasil dan Analisis Sensitivitas
Setelah menyelesaikan permasalahan program linear dan memperoleh solusi optimal, langkah selanjutnya adalah menginterpretasikan hasil tersebut dan menganalisis sensitivitasnya. Interpretasi hasil meliputi pemahaman nilai optimum fungsi objektif dan nilai variabel keputusan yang memberikan nilai optimum tersebut. Analisis sensitivitas, di sisi lain, menyelidiki bagaimana perubahan pada parameter masalah mempengaruhi solusi optimal yang telah diperoleh. Kedua langkah ini krusial untuk memastikan solusi yang diperoleh relevan dan robust terhadap perubahan kondisi.
Interpretasi Hasil Program Linear
Interpretasi hasil program linear berfokus pada dua hal utama: nilai optimum fungsi objektif dan nilai variabel keputusan pada saat optimum tercapai. Nilai optimum fungsi objektif menunjukkan nilai maksimum (untuk masalah maksimisasi) atau minimum (untuk masalah minimisasi) yang dapat dicapai, sesuai dengan kendala yang diberikan. Nilai variabel keputusan pada saat optimum menunjukkan kombinasi jumlah setiap variabel yang menghasilkan nilai optimum tersebut.
Sebagai contoh, jika kita memaksimalkan keuntungan produksi dengan variabel x (jumlah produk A) dan y (jumlah produk B), nilai optimum x dan y menunjukkan jumlah masing-masing produk yang harus diproduksi untuk mencapai keuntungan maksimum.
Contoh Interpretasi Hasil
Misalkan kita memiliki masalah program linear yang bertujuan memaksimalkan keuntungan dari produksi dua jenis kue, kue A dan kue B. Setelah diselesaikan, diperoleh solusi optimal dengan nilai fungsi objektif (keuntungan) sebesar Rp 1.500.000 dan nilai variabel keputusan x = 100 (jumlah kue A) dan y = 200 (jumlah kue B). Interpretasinya adalah keuntungan maksimum yang dapat dicapai adalah Rp 1.500.000, dan hal tersebut dicapai dengan memproduksi 100 kue A dan 200 kue B.
Setiap perubahan jumlah produksi di luar nilai x dan y ini akan mengakibatkan penurunan keuntungan.
Analisis Sensitivitas dalam Program Linear
Analisis sensitivitas merupakan proses mengevaluasi bagaimana perubahan kecil pada parameter-parameter masalah (seperti koefisien fungsi objektif atau kendala) mempengaruhi solusi optimal. Tujuannya adalah untuk mengukur seberapa sensitif solusi terhadap perubahan tersebut dan untuk mengidentifikasi parameter yang paling berpengaruh terhadap solusi optimal. Hal ini penting karena data dalam dunia nyata seringkali tidak pasti dan rentan terhadap perubahan.
Contoh Analisis Sensitivitas
Melanjutkan contoh produksi kue sebelumnya, mari kita analisis sensitivitas terhadap perubahan harga jual kue A. Misalnya, jika harga jual kue A naik sebesar 10%, kita dapat menghitung kembali solusi optimal. Jika solusi optimal berubah secara signifikan (misalnya, jumlah kue A yang diproduksi meningkat drastis), maka dapat disimpulkan bahwa model cukup sensitif terhadap perubahan harga jual kue A. Sebaliknya, jika perubahan solusi optimal relatif kecil, maka model relatif tidak sensitif terhadap perubahan tersebut.
Analisis serupa dapat dilakukan terhadap perubahan harga jual kue B, biaya produksi, atau ketersediaan bahan baku.
Poin-Penting dalam Analisis Sensitivitas, Contoh soal program linear
- Identifikasi parameter yang paling berpengaruh terhadap solusi optimal.
- Tentukan rentang perubahan parameter yang masih menghasilkan solusi optimal yang sama.
- Evaluasi dampak perubahan parameter terhadap nilai optimum fungsi objektif dan nilai variabel keputusan.
- Gunakan informasi sensitivitas untuk membuat keputusan yang lebih baik dan robust.
- Pertimbangkan ketidakpastian data dan asumsi yang mendasari model.
Aplikasi Program Linear dalam Berbagai Bidang

Program linear, sebagai metode matematis untuk optimasi, memiliki aplikasi luas dalam berbagai sektor. Kemampuannya dalam menemukan solusi terbaik dari suatu masalah dengan batasan-batasan tertentu membuatnya menjadi alat yang sangat berharga dalam pengambilan keputusan. Berikut beberapa contoh penerapannya di berbagai bidang.
Penerapan Program Linear dalam Bidang Ekonomi
Dalam bidang ekonomi, program linear sering digunakan untuk mengoptimalkan alokasi sumber daya. Misalnya, sebuah perusahaan manufaktur memiliki beberapa pabrik yang memproduksi berbagai jenis produk. Dengan menggunakan program linear, perusahaan dapat menentukan jumlah produk yang harus diproduksi di setiap pabrik agar dapat memaksimalkan keuntungan, dengan mempertimbangkan keterbatasan sumber daya seperti bahan baku, tenaga kerja, dan kapasitas produksi masing-masing pabrik. Model program linear akan memperhitungkan harga jual setiap produk, biaya produksi di setiap pabrik, dan ketersediaan sumber daya.
Solusi optimal yang dihasilkan akan menunjukkan jumlah unit setiap produk yang harus diproduksi di setiap pabrik untuk mencapai keuntungan maksimum.
Penerapan Program Linear dalam Bidang Manajemen
Di bidang manajemen, program linear membantu dalam berbagai proses pengambilan keputusan, termasuk penjadwalan produksi. Bayangkan sebuah perusahaan yang memproduksi beberapa jenis produk dengan mesin-mesin yang memiliki kapasitas terbatas. Program linear dapat digunakan untuk menentukan jadwal produksi yang optimal yang memaksimalkan output, mempertimbangkan waktu setup mesin, waktu proses produksi, dan permintaan pasar untuk setiap produk. Dengan demikian, perusahaan dapat meminimalkan waktu henti mesin dan memaksimalkan efisiensi produksi.
Penerapan Program Linear dalam Bidang Teknik
Dalam bidang teknik, program linear berperan penting dalam optimasi desain. Contohnya, dalam desain struktur bangunan, program linear dapat digunakan untuk menentukan dimensi optimal dari balok penyangga agar struktur bangunan kuat dan tahan terhadap beban, sambil meminimalkan penggunaan material. Model program linear akan memperhitungkan kekuatan material, beban yang akan ditahan, dan batasan biaya. Solusi optimal akan memberikan dimensi balok yang memenuhi persyaratan kekuatan dan efisiensi biaya.
Keuntungan dan Keterbatasan Program Linear
Program linear menawarkan beberapa keuntungan signifikan. Pertama, ia memberikan solusi optimal yang terukur dan terdokumentasi dengan baik. Kedua, metode ini relatif mudah dipahami dan diimplementasikan, terutama dengan bantuan perangkat lunak. Ketiga, program linear dapat menangani masalah dengan banyak variabel dan kendala, memberikan solusi yang komprehensif. Namun, program linear juga memiliki keterbatasan.
Model program linear seringkali menyederhanakan realitas kompleks menjadi asumsi-asumsi yang mungkin tidak sepenuhnya akurat. Selain itu, program linear hanya efektif untuk masalah optimasi linear, dan tidak dapat menangani masalah non-linear.
Ringkasan Manfaat Program Linear dalam Pengambilan Keputusan
Program linear merupakan alat yang ampuh dalam pengambilan keputusan yang efektif dan efisien. Dengan kemampuannya dalam mengoptimalkan sumber daya dan memaksimalkan output, program linear membantu organisasi untuk mencapai tujuannya dengan cara yang terukur dan terstruktur. Meskipun memiliki keterbatasan, manfaatnya dalam berbagai bidang tetap signifikan, khususnya dalam situasi di mana terdapat banyak variabel dan kendala yang harus dipertimbangkan.
Terakhir
Memahami program linear bukan hanya sekadar mempelajari rumus dan metode, tetapi juga tentang bagaimana mengaplikasikannya untuk memecahkan masalah nyata. Dengan menguasai berbagai teknik penyelesaian dan memahami interpretasi hasilnya, Anda akan mampu mengambil keputusan yang lebih efektif dan efisien dalam berbagai situasi. Semoga contoh soal dan penjelasan di atas memberikan landasan yang kuat bagi Anda dalam mempelajari program linear lebih lanjut.






