- Pengertian Limit Fungsi Trigonometri
- Teknik Penyelesaian Limit Fungsi Trigonometri
-
Contoh Soal dan Pembahasan Limit Fungsi Trigonometri
- Contoh Soal 1: Limit Fungsi Trigonometri Sederhana
- Contoh Soal 2: Limit Fungsi Trigonometri dengan Manipulasi Aljabar
- Contoh Soal 3: Limit Fungsi Trigonometri dengan Identitas Trigonometri
- Contoh Soal 4: Limit Fungsi Trigonometri dengan Bentuk Tak Tentu yang Lebih Kompleks
- Contoh Soal 5: Limit Fungsi Trigonometri yang Melibatkan Beberapa Fungsi Trigonometri
- Tabel Ringkasan Contoh Soal dan Jawaban, Contoh soal limit fungsi trigonometri
- Penerapan Limit Fungsi Trigonometri
- Kesalahan Umum dalam Menyelesaikan Limit Fungsi Trigonometri: Contoh Soal Limit Fungsi Trigonometri
- Penutupan
Contoh soal limit fungsi trigonometri merupakan topik penting dalam kalkulus. Memahami limit fungsi trigonometri membuka pintu untuk menguasai konsep-konsep lanjutan dalam matematika dan aplikasinya di berbagai bidang seperti fisika dan teknik. Artikel ini akan membahas secara rinci berbagai teknik penyelesaian limit fungsi trigonometri, mulai dari definisi dasar hingga penerapannya dalam pemecahan masalah nyata. Dengan contoh soal dan pembahasan langkah demi langkah, diharapkan pembaca dapat memahami dan menguasai materi ini dengan baik.
Kita akan menjelajahi berbagai metode penyelesaian, termasuk penggunaan identitas trigonometri, aturan L’Hopital, dan substitusi. Selain itu, akan dibahas pula kesalahan-kesalahan umum yang sering terjadi dan bagaimana cara mengatasinya. Dengan pemahaman yang komprehensif, Anda akan siap menghadapi berbagai tantangan soal limit fungsi trigonometri dengan percaya diri.
Pengertian Limit Fungsi Trigonometri
Limit fungsi trigonometri merupakan konsep matematika yang mengkaji perilaku suatu fungsi trigonometri ketika variabel bebas mendekati nilai tertentu. Konsep ini serupa dengan limit fungsi aljabar, namun objek yang dikaji adalah fungsi-fungsi trigonometri seperti sinus, kosinus, tangen, dan turunannya. Pemahaman limit fungsi trigonometri sangat penting dalam kalkulus dan aplikasinya di berbagai bidang, termasuk fisika dan teknik.
Definisi Limit Fungsi Trigonometri
Secara formal, limit fungsi trigonometri f(x) ketika x mendekati a ditulis sebagai:
limx→a f(x) = L
dimana L adalah nilai limit. Artinya, nilai fungsi f(x) akan mendekati L ketika x semakin dekat ke a, tanpa harus sama dengan a. Dalam konteks fungsi trigonometri, f(x) dapat berupa fungsi sinus, kosinus, tangen, atau kombinasi dari fungsi-fungsi tersebut.
Contoh Limit Fungsi Trigonometri
Mari kita tinjau contoh sederhana. Misalnya, kita ingin mencari limit dari fungsi f(x) = sin(x) ketika x mendekati 0:
limx→0 sin(x) = 0
Nilai sin(x) akan mendekati 0 ketika x mendekati 0. Hal ini dapat diverifikasi dengan substitusi nilai x yang mendekati 0 (misalnya, 0.1, 0.01, 0.001, dan seterusnya) ke dalam fungsi sin(x). Semakin dekat x ke 0, semakin dekat nilai sin(x) ke 0.
Perbedaan Limit Fungsi Trigonometri dan Limit Fungsi Aljabar
Meskipun prinsip dasar limit sama, terdapat perbedaan dalam penerapannya pada fungsi trigonometri dan fungsi aljabar. Limit fungsi aljabar seringkali dapat diselesaikan dengan substitusi langsung, sementara limit fungsi trigonometri seringkali membutuhkan manipulasi aljabar atau penggunaan identitas trigonometri untuk mendapatkan bentuk yang lebih sederhana sebelum substitusi. Selain itu, fungsi trigonometri bersifat periodik, sehingga perilaku limitnya dapat berbeda dibandingkan dengan fungsi aljabar yang umumnya bersifat monoton atau memiliki perilaku yang lebih sederhana.
Tabel Perbandingan Limit Fungsi Trigonometri dan Limit Fungsi Aljabar
Berikut tabel perbandingan yang menyoroti perbedaan antara limit fungsi trigonometri dan limit fungsi aljabar:
| Jenis Fungsi | Definisi | Contoh | Perbedaan |
|---|---|---|---|
| Trigonometri | Mencari nilai pendekatan fungsi trigonometri saat variabel mendekati nilai tertentu. | limx→0 sin(x)/x = 1 | Seringkali memerlukan manipulasi trigonometri dan identitas. |
| Aljabar | Mencari nilai pendekatan fungsi aljabar saat variabel mendekati nilai tertentu. | limx→2 (x²
|
Seringkali dapat diselesaikan dengan substitusi langsung. |
Ilustrasi Grafik Fungsi Trigonometri dan Konsep Limit
Perhatikan grafik fungsi f(x) = sin(x). Grafik ini berbentuk gelombang yang berosilasi antara -1 dan 1. Jika kita perhatikan perilaku grafik di sekitar titik x = 0, kita akan melihat bahwa nilai f(x) mendekati 0 ketika x mendekati 0 dari kiri maupun dari kanan. Titik kritis di sini adalah x = 0, dan nilai limitnya adalah 0.
Grafik tersebut menunjukkan bagaimana nilai fungsi mendekati nilai limit tertentu (dalam hal ini 0) saat variabel bebas mendekati titik kritis, meskipun nilai fungsi di titik kritis itu sendiri mungkin berbeda (atau bahkan tidak terdefinisi).
Sebagai contoh lain, perhatikan fungsi f(x) = tan(x). Grafik fungsi tangen memiliki asimtot vertikal pada x = π/2 + kπ, di mana k adalah bilangan bulat. Limit fungsi tangen ketika x mendekati π/2 dari kiri akan menuju tak hingga positif (∞), sedangkan limit ketika x mendekati π/2 dari kanan akan menuju tak hingga negatif (-∞). Ini menunjukkan bahwa limit di titik-titik asimtot vertikal tidak ada.
Teknik Penyelesaian Limit Fungsi Trigonometri
Menentukan limit fungsi trigonometri seringkali membutuhkan pendekatan khusus. Keberadaan fungsi trigonometri dan kemungkinan bentuk tak tentu (seperti 0/0 atau ∞/∞) menuntut pemahaman yang baik terhadap identitas trigonometri, aturan L’Hopital, dan teknik substitusi. Pemilihan teknik yang tepat akan menyederhanakan proses perhitungan dan menghasilkan solusi yang akurat.
Berikut ini akan dijelaskan beberapa teknik penyelesaian limit fungsi trigonometri beserta contoh penerapannya.
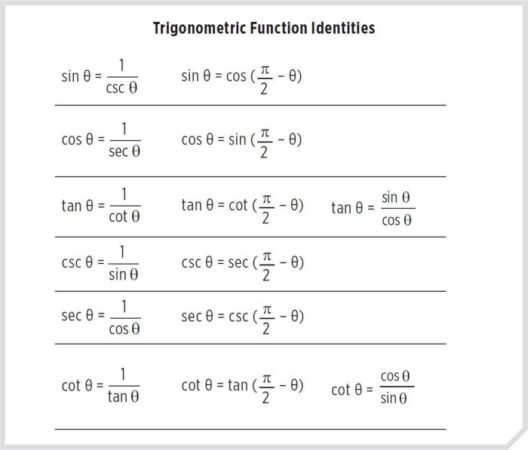
Menggunakan Identitas Trigonometri
Identitas trigonometri merupakan alat yang ampuh untuk menyederhanakan ekspresi trigonometri yang kompleks sebelum menghitung limit. Dengan menggunakan identitas seperti sin 2x = 2 sin x cos x, cos 2x = cos²x – sin²x, atau lim (sin x)/x = 1 (untuk x mendekati 0), kita dapat mengubah bentuk fungsi sehingga limitnya dapat dihitung secara langsung atau dengan substitusi sederhana.
Contoh soal: Tentukan nilai lim x→0 (sin 2x) / x
Penyelesaian: Dengan menggunakan identitas sin 2x = 2 sin x cos x, soal di atas dapat diubah menjadi:
limx→0 (2 sin x cos x) / x = lim x→0 2 (sin x / x) cos x
Karena lim x→0 (sin x / x) = 1 dan lim x→0 cos x = 1, maka:
limx→0 (sin 2x) / x = 2 (1)(1) = 2
Menggunakan Aturan L’Hopital
Aturan L’Hopital sangat berguna ketika kita menghadapi bentuk tak tentu seperti 0/0 atau ∞/∞. Aturan ini menyatakan bahwa jika lim x→a f(x) / g(x) berbentuk tak tentu, maka lim x→a f(x) / g(x) = lim x→a f'(x) / g'(x), dengan syarat limit di ruas kanan ada.
Contoh soal: Tentukan nilai lim x→0 (sin x) / x
Penyelesaian: Bentuk ini merupakan bentuk tak tentu 0/
0. Dengan menggunakan aturan L’Hopital:
limx→0 (sin x) / x = lim x→0 (cos x) / 1 = cos 0 = 1
Menggunakan Metode Substitusi
Metode substitusi melibatkan penggantian variabel dengan ekspresi lain yang setara untuk menyederhanakan fungsi sebelum menghitung limit. Teknik ini efektif ketika terdapat fungsi komposit atau fungsi yang dapat disederhanakan dengan substitusi yang tepat.
Contoh soal: Tentukan nilai lim x→π/2 (cos x) / (π/2 – x)
Penyelesaian: Misalkan u = π/2 – x. Ketika x mendekati π/2, u mendekati
0. Maka cos x = cos(π/2 – u) = sin u. Persamaan menjadi:
limu→0 (sin u) / u = 1
Alur Penyelesaian Limit Fungsi Trigonometri
Berikut flowchart alur penyelesaian limit fungsi trigonometri yang mencakup berbagai teknik yang telah dijelaskan di atas:
- Identifikasi bentuk limit: Apakah limit berbentuk tak tentu (0/0, ∞/∞, dll.) atau dapat dihitung langsung dengan substitusi?
- Jika bentuk tak tentu:
- Coba sederhanakan menggunakan identitas trigonometri.
- Jika masih bentuk tak tentu, gunakan aturan L’Hopital.
- Jika bukan bentuk tak tentu: Gunakan substitusi langsung untuk menghitung limit.
- Sederhanakan hasil: Pastikan hasil akhir dalam bentuk yang paling sederhana.
Contoh Soal dan Pembahasan Limit Fungsi Trigonometri
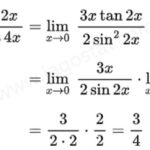
Limit fungsi trigonometri merupakan konsep penting dalam kalkulus yang melibatkan pencarian nilai pendekatan suatu fungsi trigonometri ketika variabel mendekati nilai tertentu. Memahami konsep limit ini sangat krusial untuk mempelajari konsep turunan dan integral selanjutnya. Berikut beberapa contoh soal dan pembahasannya untuk mengilustrasikan berbagai teknik penyelesaian.
Contoh Soal 1: Limit Fungsi Trigonometri Sederhana
Soal ini membahas limit fungsi trigonometri dasar yang dapat diselesaikan dengan substitusi langsung.
Tentukan nilai dari lim x→0 sin x / x
- Substitusikan nilai x = 0 ke dalam fungsi: sin 0 / 0 = 0/0 (bentuk tak tentu).
- Gunakan aturan L’Hôpital (menurunkan pembilang dan penyebut): limx→0 cos x / 1 = cos 0 / 1 = 1
Aturan L’Hôpital digunakan untuk menyelesaikan limit yang berbentuk tak tentu 0/0 atau ∞/∞. Aturan ini menyatakan bahwa limit dari hasil bagi dua fungsi yang dapat diturunkan sama dengan limit dari hasil bagi turunannya.
Ranguman:
- Bentuk soal: Limit fungsi trigonometri sederhana.
- Metode: Aturan L’Hôpital.
- Jawaban: 1
Contoh Soal 2: Limit Fungsi Trigonometri dengan Manipulasi Aljabar
Soal ini memerlukan manipulasi aljabar sebelum substitusi nilai x.
Tentukan nilai dari lim x→π/2 (1 – sin x) / (π/2 – x)
- Substitusi langsung menghasilkan bentuk tak tentu 0/0.
- Gunakan identitas trigonometri atau manipulasi aljabar untuk menyederhanakan fungsi.
- Misalkan u = π/2 – x, maka x = π/2 – u. Ketika x → π/2, u → 0. Fungsi menjadi limu→0 (1 – sin(π/2 – u)) / u = lim u→0 (1 – cos u) / u.
- Bentuk ini masih 0/0, gunakan aturan L’Hôpital: lim u→0 sin u / 1 = sin 0 / 1 = 0
Dalam menyelesaikan limit fungsi trigonometri, manipulasi aljabar dan identitas trigonometri seringkali diperlukan untuk mengubah fungsi ke bentuk yang lebih mudah dikerjakan.
Ranguman:
- Bentuk soal: Limit fungsi trigonometri yang memerlukan manipulasi aljabar.
- Metode: Substitusi variabel dan aturan L’Hôpital.
- Jawaban: 0
Contoh Soal 3: Limit Fungsi Trigonometri dengan Identitas Trigonometri
Soal ini menekankan penggunaan identitas trigonometri untuk penyederhanaan.
Tentukan nilai dari lim x→0 (tan x) / x
- Substitusi langsung menghasilkan bentuk tak tentu 0/0.
- Gunakan identitas tan x = sin x / cos x: limx→0 (sin x / cos x) / x = lim x→0 sin x / (x cos x).
- Pisahkan limit: lim x→0 (sin x / x)
- lim x→0 (1 / cos x) = 1
- 1 = 1
Identitas trigonometri seperti sin2x + cos 2x = 1, tan x = sin x / cos x, dan lainnya sangat membantu dalam penyederhanaan fungsi trigonometri sebelum menghitung limit.
Ranguman:
- Bentuk soal: Limit fungsi trigonometri yang melibatkan identitas trigonometri.
- Metode: Identitas trigonometri dan sifat limit.
- Jawaban: 1
Contoh Soal 4: Limit Fungsi Trigonometri dengan Bentuk Tak Tentu yang Lebih Kompleks
Soal ini memperlihatkan penyelesaian limit dengan bentuk tak tentu yang lebih rumit.
Tentukan nilai dari lim x→0 (1 – cos x) / x 2
- Substitusi langsung menghasilkan bentuk tak tentu 0/0.
- Gunakan aturan L’Hôpital: limx→0 sin x / (2x) (masih 0/0).
- Gunakan aturan L’Hôpital lagi: lim x→0 cos x / 2 = cos 0 / 2 = 1/2
Penggunaan berulang aturan L’Hôpital mungkin diperlukan untuk beberapa kasus limit fungsi trigonometri yang kompleks.
Ranguman:
- Bentuk soal: Limit fungsi trigonometri dengan bentuk tak tentu 0/0 yang memerlukan aplikasi berulang aturan L’Hôpital.
- Metode: Aturan L’Hôpital (berulang).
- Jawaban: 1/2
Contoh Soal 5: Limit Fungsi Trigonometri yang Melibatkan Beberapa Fungsi Trigonometri
Soal ini menggabungkan beberapa fungsi trigonometri dalam satu limit.
Tentukan nilai dari lim x→0 (sin 2x + tan x) / x
- Pisahkan limit: limx→0 (sin 2x / x) + lim x→0 (tan x / x).
- Untuk lim x→0 (sin 2x / x), kalikan dan bagi dengan 2: lim x→0 2 (sin 2x / 2x) = 2 – 1 = 2.
- Untuk lim x→0 (tan x / x), gunakan identitas tan x = sin x / cos x dan pisahkan limit seperti pada soal sebelumnya: 1.
- Jumlahkan kedua limit: 2 + 1 = 3
Beberapa limit fungsi trigonometri dapat diselesaikan dengan memisahkan limit menjadi beberapa bagian yang lebih sederhana.
Ranguman:
- Bentuk soal: Limit fungsi trigonometri yang melibatkan penjumlahan beberapa fungsi trigonometri.
- Metode: Pemisahan limit dan penggunaan sifat limit.
- Jawaban: 3
Tabel Ringkasan Contoh Soal dan Jawaban, Contoh soal limit fungsi trigonometri
| No. | Soal | Jawaban |
|---|---|---|
| 1 | limx→0 sin x / x | 1 |
| 2 | limx→π/2 (1 – sin x) / (π/2 – x) | 0 |
| 3 | limx→0 (tan x) / x | 1 |
| 4 | limx→0 (1 – cos x) / x2 | 1/2 |
| 5 | limx→0 (sin 2x + tan x) / x | 3 |
Penerapan Limit Fungsi Trigonometri
Limit fungsi trigonometri, meskipun tampak abstrak, memiliki aplikasi yang luas dan mendalam dalam berbagai bidang ilmu. Konsep ini memungkinkan kita untuk menganalisis perilaku fungsi trigonometri ketika variabel mendekati nilai tertentu, memberikan pemahaman yang lebih akurat tentang fenomena periodik dan perubahan yang terjadi secara bertahap.
Penerapannya meluas dari perhitungan yang presisi dalam fisika hingga desain yang efisien dalam teknik. Pemahaman yang kuat tentang limit fungsi trigonometri menjadi kunci dalam menyelesaikan masalah-masalah kompleks dan mengoptimalkan berbagai proses.
Aplikasi Limit Fungsi Trigonometri dalam Matematika dan Ilmu Terapan
Limit fungsi trigonometri merupakan fondasi penting dalam kalkulus lanjutan, khususnya dalam pengembangan konsep turunan dan integral fungsi trigonometri. Konsep ini juga berperan krusial dalam analisis Fourier, yang digunakan untuk mendekomposisi fungsi periodik menjadi jumlah dari fungsi sinus dan kosinus. Analisis Fourier memiliki aplikasi luas dalam pemrosesan sinyal, pengolahan citra, dan mekanika kuantum.
- Perhitungan luas daerah di bawah kurva fungsi trigonometri.
- Penentuan kecepatan dan percepatan dalam gerak harmonik sederhana.
- Analisis gelombang dan fenomena periodik lainnya.
Penerapan Limit Fungsi Trigonometri dalam Fisika
Dalam fisika, limit fungsi trigonometri digunakan untuk menganalisis gerak osilasi, seperti gerak pendulum sederhana. Ketika amplitudo osilasi kecil, perilaku pendulum dapat dimodelkan dengan menggunakan fungsi trigonometri, dan limit digunakan untuk menentukan kecepatan dan percepatan pada titik-titik tertentu dalam osilasi. Selain itu, limit juga berperan dalam analisis gelombang cahaya dan suara, membantu dalam memahami fenomena interferensi dan difraksi.
Sebagai contoh, dalam menentukan kecepatan sesaat sebuah partikel yang bergerak melingkar beraturan, kita menggunakan limit untuk menghitung turunan dari fungsi posisi yang melibatkan fungsi trigonometri.
Penerapan Limit Fungsi Trigonometri dalam Kalkulus
Limit fungsi trigonometri merupakan konsep dasar dalam kalkulus. Konsep ini digunakan untuk mendefinisikan turunan dan integral fungsi trigonometri. Turunan fungsi trigonometri digunakan untuk menentukan kecepatan perubahan fungsi, sedangkan integral fungsi trigonometri digunakan untuk menghitung luas daerah di bawah kurva.
Contohnya, penentuan turunan dari fungsi sinus (sin x) dan kosinus (cos x) sangat bergantung pada limit fungsi trigonometri. Rumus turunan tersebut kemudian digunakan dalam berbagai aplikasi kalkulus lainnya, seperti optimasi dan pemecahan persamaan diferensial.
Penerapan Limit Fungsi Trigonometri dalam Teknik
Dalam teknik, limit fungsi trigonometri digunakan dalam berbagai aplikasi, termasuk desain jembatan, bangunan, dan mesin. Konsep ini digunakan untuk menganalisis gaya dan tegangan pada struktur, serta untuk memprediksi perilaku struktur di bawah beban. Limit juga digunakan dalam desain sistem kontrol dan pemodelan sistem dinamis.
Misalnya, dalam desain jembatan gantung, perhitungan tegangan kabel dan momen lentur balok menggunakan model matematika yang melibatkan fungsi trigonometri, dan analisis limit digunakan untuk memastikan struktur jembatan mampu menahan beban yang diberikan.
Skenario Permasalahan Nyata yang Diselesaikan dengan Limit Fungsi Trigonometri
Bayangkan sebuah perahu yang bergerak naik turun mengikuti gelombang laut. Gerakan naik turun ini dapat dimodelkan dengan fungsi trigonometri. Untuk menentukan kecepatan perahu pada suatu titik waktu tertentu, kita dapat menggunakan konsep limit untuk menghitung turunan dari fungsi posisi perahu. Dengan mengetahui kecepatan sesaat, kita dapat memprediksi posisi perahu di masa mendatang dan menghindari potensi bahaya.
Contoh lain, dalam desain antena parabola, geometri parabola didefinisikan menggunakan fungsi trigonometri. Analisis limit digunakan untuk mengoptimalkan desain antena agar dapat menerima dan mengirimkan sinyal dengan efisiensi maksimum. Ini memastikan kualitas sinyal yang optimal dan jangkauan transmisi yang luas.
Kesalahan Umum dalam Menyelesaikan Limit Fungsi Trigonometri: Contoh Soal Limit Fungsi Trigonometri

Menentukan limit fungsi trigonometri membutuhkan pemahaman yang kuat tentang identitas trigonometri dan teknik aljabar. Meskipun terlihat sederhana, beberapa kesalahan umum seringkali menghambat proses penyelesaian. Memahami kesalahan-kesalahan ini dan cara mengatasinya akan meningkatkan kemampuan dalam menyelesaikan soal limit fungsi trigonometri dengan akurat dan efisien.
Penggunaan Identitas Trigonometri yang Salah
Salah satu kesalahan umum adalah penggunaan identitas trigonometri yang tidak tepat atau salah. Seringkali, siswa keliru dalam menerapkan rumus-rumus seperti sin 2x = 2 sin x cos x atau cos 2x = cos²x – sin²x, atau bahkan lupa mempertimbangkan domain dan range fungsi trigonometri. Kesalahan ini dapat menyebabkan hasil limit yang salah secara signifikan.
Contohnya, dalam menyelesaikan lim x→0 (sin 2x) / x, beberapa siswa mungkin salah menggunakan identitas sin 2x = 2 sin x, sehingga menghasilkan hasil yang keliru. Penggunaan identitas yang tepat adalah sin 2x = 2 sin x cos x, kemudian dilanjutkan dengan manipulasi aljabar dan limit dasar lim x→0 (sin x) / x = 1.
Untuk menghindari kesalahan ini, pastikan untuk memahami dan mengingat dengan benar identitas trigonometri yang relevan, serta memeriksa kembali langkah-langkah yang dilakukan agar terhindar dari kesalahan kalkulasi.
Pengabaian Aturan L’Hôpital
Aturan L’Hôpital merupakan alat yang ampuh dalam menyelesaikan limit fungsi trigonometri yang berbentuk tak tentu, seperti 0/0 atau ∞/∞. Namun, beberapa siswa mengabaikan aturan ini atau menerapkannya secara tidak tepat, misalnya dengan langsung menurunkan pembilang dan penyebut tanpa memeriksa terlebih dahulu apakah bentuk limit tersebut memenuhi syarat penggunaan aturan L’Hôpital.
Contohnya, limit lim x→0 (sin x) / x dapat diselesaikan dengan aturan L’Hôpital dengan menurunkan pembilang dan penyebut menjadi cos x / 1, sehingga limitnya menjadi cos 0 = 1. Namun, perlu diingat bahwa aturan L’Hôpital hanya berlaku untuk bentuk tak tentu. Jika bentuk limit bukan bentuk tak tentu, aturan L’Hôpital tidak dapat digunakan.
Cara menghindari kesalahan ini adalah dengan selalu memeriksa terlebih dahulu apakah bentuk limit memenuhi syarat penggunaan aturan L’Hôpital sebelum menerapkannya. Jika tidak, carilah metode alternatif seperti manipulasi aljabar atau penggunaan identitas trigonometri.
Kesalahan dalam Manipulasi Aljabar
Penyelesaian limit fungsi trigonometri seringkali melibatkan manipulasi aljabar, seperti pemfaktoran, penyederhanaan pecahan, dan penggunaan identitas trigonometri. Kesalahan dalam manipulasi aljabar ini dapat mengakibatkan hasil limit yang salah. Kesalahan umum meliputi kesalahan tanda, kesalahan dalam perkalian atau pembagian, dan kesalahan dalam pemfaktoran.
Contohnya, dalam menyelesaikan limit yang melibatkan bentuk tak tentu, kesalahan dalam manipulasi aljabar dapat menyebabkan penyederhanaan yang salah dan menghasilkan limit yang salah. Perlu ketelitian dan kehati-hatian dalam setiap langkah manipulasi aljabar.
Untuk menghindari kesalahan ini, selalu periksa kembali setiap langkah manipulasi aljabar. Usahakan untuk menuliskan langkah-langkah dengan rapi dan jelas, sehingga memudahkan dalam mendeteksi kesalahan.
Panduan Langkah Demi Langkah Menyelesaikan Limit Fungsi Trigonometri
- Identifikasi bentuk limit. Apakah limit tersebut berbentuk tak tentu (0/0, ∞/∞, dll.) atau tidak?
- Jika berbentuk tak tentu, pertimbangkan penggunaan aturan L’Hôpital. Pastikan syarat penggunaannya terpenuhi.
- Jika tidak berbentuk tak tentu, atau jika aturan L’Hôpital tidak dapat diterapkan, gunakan identitas trigonometri dan manipulasi aljabar untuk menyederhanakan fungsi.
- Substitusikan nilai x yang mendekati titik limit ke dalam fungsi yang telah disederhanakan.
- Periksa kembali setiap langkah untuk memastikan keakuratan.
Kesalahan Umum dan Cara Mengatasinya
| Kesalahan Umum | Cara Mengatasi |
|---|---|
| Penggunaan identitas trigonometri yang salah | Pastikan pemahaman dan penggunaan identitas trigonometri yang benar. Periksa kembali setiap langkah. |
| Pengabaian atau penerapan aturan L’Hôpital yang salah | Periksa terlebih dahulu apakah bentuk limit memenuhi syarat penggunaan aturan L’Hôpital. Jika ya, terapkan dengan benar. Jika tidak, gunakan metode lain. |
| Kesalahan dalam manipulasi aljabar | Tuliskan langkah-langkah dengan rapi dan jelas. Periksa kembali setiap langkah untuk menghindari kesalahan tanda, perkalian, atau pembagian. |
Penutupan
Setelah mempelajari berbagai contoh soal dan teknik penyelesaian limit fungsi trigonometri, diharapkan pemahaman Anda semakin mendalam. Kemampuan untuk mengaplikasikan berbagai metode, mulai dari identitas trigonometri hingga aturan L’Hopital, akan sangat bermanfaat dalam menyelesaikan soal-soal yang lebih kompleks. Ingatlah untuk selalu teliti dalam setiap langkah dan memahami konsep dasar di balik setiap metode. Dengan latihan yang konsisten, Anda akan mampu menguasai materi ini dan siap menghadapi tantangan berikutnya dalam dunia kalkulus.