Contoh soal dilatasi merupakan pintu gerbang untuk memahami transformasi geometri yang menarik ini. Dilatasi, atau perbesaran, merupakan transformasi geometri yang mengubah ukuran suatu objek tanpa mengubah bentuknya. Bayangkan sebuah foto yang diperbesar atau diperkecil – itulah konsep dasar dilatasi. Dalam pembahasan ini, kita akan menjelajahi berbagai contoh soal dilatasi, mulai dari yang sederhana hingga yang lebih kompleks, lengkap dengan penyelesaian langkah demi langkah.
Kita akan mempelajari rumus dan prosedur dilatasi, serta mengaplikasikannya pada berbagai bangun geometri. Selain itu, akan dibahas pula perbedaan dilatasi dengan transformasi geometri lainnya seperti translasi dan rotasi. Dengan pemahaman yang komprehensif, Anda akan mampu menyelesaikan berbagai soal dilatasi dengan mudah dan percaya diri.
Pengertian Dilatasi
Dilatasi dalam geometri transformasi merupakan suatu transformasi geometri yang mengubah ukuran suatu objek tanpa mengubah bentuknya. Transformasi ini dilakukan dengan memperbesar atau memperkecil objek terhadap suatu titik pusat yang disebut titik pusat dilatasi. Ukuran perubahan objek ditentukan oleh suatu nilai yang disebut faktor skala.
Contoh Dilatasi dengan Faktor Skala Positif dan Negatif
Faktor skala menentukan seberapa besar objek diperbesar atau diperkecil. Faktor skala positif menunjukkan pembesaran, sedangkan faktor skala negatif menunjukkan pembesaran disertai pencerminan terhadap titik pusat dilatasi. Sebagai contoh, dilatasi dengan faktor skala 2 terhadap titik pusat (0,0) akan memperbesar objek dua kali lipat ukuran aslinya. Sementara itu, dilatasi dengan faktor skala -2 akan memperbesar objek dua kali lipat dan kemudian mencerminkan objek tersebut terhadap titik pusat (0,0).
Ilustrasi Dilatasi dengan Faktor Skala 2 terhadap Titik Pusat (0,0)
Misalkan kita memiliki titik A(1,1). Dilatasi dengan faktor skala 2 terhadap titik pusat (0,0) akan memetakan titik A ke titik A'(2,2). Proses transformasinya adalah dengan mengalikan koordinat titik A dengan faktor skala 2. Jadi, koordinat x dan y dari titik A dikalikan 2, menghasilkan koordinat x’ = 2(1) = 2 dan y’ = 2(1) = 2. Dengan demikian, titik A(1,1) dipetakan ke A'(2,2).
Bayangkan titik A sebagai sebuah titik kecil pada bidang koordinat. Dilatasi ini seolah-olah “menarik” titik A menjauhi titik pusat (0,0) sehingga jaraknya menjadi dua kali lipat. Bentuknya tetap berupa titik, hanya ukuran jaraknya dari titik pusat yang berubah.
Perbedaan Dilatasi dengan Faktor Skala Lebih dari 1 dan Kurang dari 1
Dilatasi dengan faktor skala lebih dari 1 akan menghasilkan bayangan yang lebih besar dari objek aslinya (pembesaran). Sebaliknya, dilatasi dengan faktor skala antara 0 dan 1 akan menghasilkan bayangan yang lebih kecil dari objek aslinya (pemperkecilan). Faktor skala 1 akan menghasilkan bayangan yang identik dengan objek aslinya.
Perbandingan Dilatasi dengan Translasi dan Rotasi
| Transformasi | Penjelasan | Contoh |
|---|---|---|
| Dilatasi | Mengubah ukuran objek tanpa mengubah bentuknya. | Memperbesar atau memperkecil gambar pada peta. |
| Translasi | Memindahkan objek tanpa mengubah ukuran atau bentuknya. | Menggeser objek beberapa satuan ke kiri, kanan, atas, atau bawah. |
| Rotasi | Memutar objek terhadap suatu titik pusat tanpa mengubah ukuran atau bentuknya. | Memutar roda sepeda. |
Perbedaan utama antara dilatasi dengan translasi dan rotasi terletak pada perubahan ukuran objek. Dilatasi mengubah ukuran, sedangkan translasi dan rotasi hanya mengubah posisi objek tanpa mengubah ukuran atau bentuknya.
Rumus dan Prosedur Dilatasi
Dilatasi merupakan transformasi geometri yang mengubah ukuran suatu objek tanpa mengubah bentuknya. Proses ini dilakukan dengan memperbesar atau memperkecil objek terhadap suatu titik pusat dengan faktor skala tertentu. Pemahaman tentang rumus dan prosedur dilatasi sangat penting dalam berbagai aplikasi geometri, termasuk dalam pemetaan, desain grafis, dan bahkan pemodelan komputer.
Rumus Dilatasi
Rumus umum untuk dilatasi terhadap titik pusat (a, b) dengan faktor skala k adalah sebagai berikut:
x’ = k(x – a) + a
y’ = k(y – b) + b
dimana (x, y) adalah koordinat titik asal dan (x’, y’) adalah koordinat bayangan titik setelah didilatasi.
Prosedur Penentuan Bayangan Titik Setelah Dilatasi
Berikut langkah-langkah untuk menentukan bayangan suatu titik setelah didilatasi:
- Tentukan koordinat titik asal (x, y).
- Tentukan koordinat titik pusat dilatasi (a, b).
- Tentukan faktor skala (k).
- Substitusikan nilai-nilai tersebut ke dalam rumus dilatasi: x’ = k(x – a) + a dan y’ = k(y – b) + b.
- Hitung nilai x’ dan y’ untuk mendapatkan koordinat bayangan (x’, y’).
Titik Asal, Titik Pusat Dilatasi, Faktor Skala, dan Bayangan Titik
Tabel berikut menunjukkan contoh perhitungan dilatasi. Tabel ini dirancang responsif, sehingga akan menyesuaikan diri dengan ukuran layar perangkat yang digunakan.
| Titik Asal (x,y) | Titik Pusat Dilatasi (a,b) | Faktor Skala (k) | Bayangan Titik (x’,y’) |
|---|---|---|---|
| (3,4) | (1,2) | 2 | (5,6) |
| (-2,1) | (0,0) | 3 | (-6,3) |
| (0,0) | (2,3) | -1 | (2,3) |
| (1,-1) | (-1,1) | 0.5 | (0,0) |
Contoh Soal Dilatasi
Berikut demonstrasi penggunaan rumus dilatasi dengan contoh soal:
Tentukan bayangan titik (3,4) setelah didilatasi dengan faktor skala 2 terhadap titik pusat (1,2).
Penyelesaian:
Dengan menggunakan rumus dilatasi:
x’ = k(x – a) + a = 2(3 – 1) + 1 = 5
y’ = k(y – b) + b = 2(4 – 2) + 2 = 6
Jadi, bayangan titik (3,4) setelah didilatasi adalah (5,6).
Contoh Soal Dilatasi dengan Titik Pusat Bukan pada Titik Asal (0,0)
Tentukan bayangan titik (-1, 2) jika didilatasi dengan faktor skala -3 terhadap titik pusat (2, -1).
Penyelesaian:
Dengan menggunakan rumus dilatasi:
x’ = -3(-1 – 2) + 2 = 11
y’ = -3(2 – (-1)) + (-1) = -10
Jadi, bayangan titik (-1, 2) setelah didilatasi adalah (11, -10).
Contoh Soal Dilatasi dan Penyelesaiannya
Dilatasi merupakan transformasi geometri yang mengubah ukuran suatu bangun geometri tanpa mengubah bentuknya. Pemahaman tentang dilatasi sangat penting dalam berbagai bidang, termasuk geometri, seni, dan bahkan pemrograman komputer. Berikut ini beberapa contoh soal dilatasi dengan tingkat kesulitan yang bervariasi, lengkap dengan penyelesaian langkah demi langkah.
Contoh Soal Dilatasi Tingkat Mudah
Sebuah titik A(2, 3) didilatasi dengan faktor skala 2 terhadap titik pusat O(0, 0). Tentukan koordinat bayangan titik A.
Langkah 1: Identifikasi titik asal A(2,3), faktor skala k=2, dan pusat dilatasi O(0,0).
Langkah 2: Gunakan rumus dilatasi: A'(x’, y’) = k(x – a) + a, k(y – b) + b, dimana (a,b) adalah pusat dilatasi dan k adalah faktor skala. Dalam kasus ini, a=0 dan b=0.
Langkah 3: Substitusikan nilai-nilai yang diketahui ke dalam rumus: x’ = 2(2 – 0) + 0 = 4 dan y’ = 2(3 – 0) + 0 = 6.
Langkah 4: Koordinat bayangan titik A adalah A'(4, 6).
Contoh Soal Dilatasi Tingkat Sedang
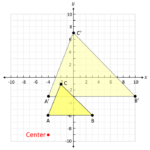
Segitiga ABC dengan koordinat A(1, 1), B(3, 1), dan C(2, 3) didilatasi dengan faktor skala -1 terhadap titik pusat P(2, 2). Tentukan koordinat bayangan segitiga ABC.
Langkah 1: Identifikasi koordinat titik sudut segitiga A(1,1), B(3,1), C(2,3), faktor skala k=-1, dan pusat dilatasi P(2,2).
Langkah 2: Gunakan rumus dilatasi yang sama seperti contoh sebelumnya, tetapi kali ini dengan pusat dilatasi P(2,2).
Langkah 3: Hitung koordinat bayangan masing-masing titik:
- A'(x’, y’) = -1(1 – 2) + 2 = 3, -1(1 – 2) + 2 = 3. Jadi A'(3, 3).
- B'(x’, y’) = -1(3 – 2) + 2 = 1, -1(1 – 2) + 2 = 3. Jadi B'(1, 3).
- C'(x’, y’) = -1(2 – 2) + 2 = 2, -1(3 – 2) + 2 = 1. Jadi C'(2, 1).
Langkah 4: Koordinat bayangan segitiga ABC adalah A'(3, 3), B'(1, 3), dan C'(2, 1).
Contoh Soal Dilatasi Tingkat Sulit (Dilatasi dan Refleksi)
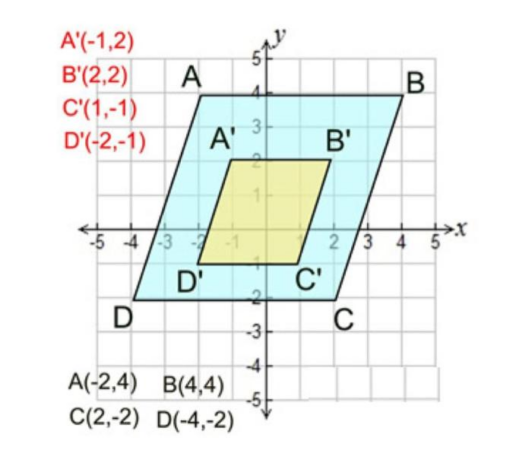
Sebuah persegi panjang ABCD dengan titik A(1, 1), B(4, 1), C(4, 3), dan D(1, 3) didilatasi dengan faktor skala 2 terhadap titik pusat O(0, 0), kemudian direfleksikan terhadap sumbu-x. Tentukan koordinat bayangan akhir persegi panjang ABCD.
Langkah 1: Tentukan bayangan setelah dilatasi. Gunakan rumus dilatasi dengan k=2 dan pusat (0,0). Kita akan mendapatkan A'(2,2), B'(8,2), C'(8,6), dan D'(2,6).
Langkah 2: Refleksi terhadap sumbu-x. Rumus refleksi terhadap sumbu-x adalah (x, -y). Dengan demikian:
- A”(2, -2)
- B”(8, -2)
- C”(8, -6)
- D”(2, -6)
Langkah 3: Koordinat bayangan akhir persegi panjang ABCD setelah dilatasi dan refleksi adalah A”(2, -2), B”(8, -2), C”(8, -6), dan D”(2, -6).
Aplikasi Dilatasi dalam Kehidupan Sehari-hari
Dilatasi, transformasi geometri yang mengubah ukuran objek tanpa mengubah bentuknya, ternyata memiliki aplikasi yang luas dalam kehidupan sehari-hari. Konsep ini, yang melibatkan pembesaran atau pengecilan suatu objek terhadap titik pusat, terlihat lebih nyata dari yang kita sadari. Berikut beberapa contoh penerapannya dalam berbagai bidang.
Penerapan Dilatasi dalam Berbagai Bidang
Dilatasi digunakan dalam berbagai bidang, mulai dari teknik sipil hingga desain grafis. Penggunaan yang beragam ini menunjukkan fleksibilitas dan pentingnya konsep dilatasi dalam memecahkan masalah praktis.
- Teknik Sipil dan Arsitektur: Dalam perencanaan dan pembangunan infrastruktur, dilatasi digunakan untuk membuat model skala bangunan atau jembatan. Arsitek menggunakan prinsip dilatasi untuk memperbesar atau memperkecil desain bangunan sebelum implementasi di lapangan, memastikan proporsi dan detail terjaga dengan akurat.
- Pemetaan dan Gambar Teknik: Dilatasi berperan penting dalam pembuatan peta. Proses pembuatan peta melibatkan penyederhanaan dan pengurangan skala suatu wilayah yang luas. Misalnya, peta suatu kota dibuat dengan skala tertentu, dimana jarak sebenarnya di daratan direpresentasikan dengan ukuran yang lebih kecil pada peta. Proses ini pada dasarnya adalah penerapan dilatasi dengan faktor skala tertentu, yang memperkecil ukuran wilayah yang dipetakan.
- Fotografi dan Desain Grafis: Dalam fotografi dan desain grafis, dilatasi diimplementasikan melalui proses pembesaran dan pengecilan gambar. Software pengolah gambar memanfaatkan prinsip dilatasi untuk memperbesar detail gambar tanpa kehilangan kualitas yang signifikan (tergantung resolusi awal). Pengecilan gambar juga menggunakan prinsip yang sama, dengan mengurangi ukuran gambar sesuai kebutuhan. Penggunaan filter atau efek tertentu juga bisa melibatkan prinsip dilatasi.
Ilustrasi Dilatasi dalam Pembuatan Peta
Bayangkan pembuatan peta sebuah taman kota. Taman tersebut memiliki panjang 100 meter dan lebar 50 meter. Untuk membuat peta yang mudah dibaca, kita perlu memperkecil ukuran taman tersebut. Misalkan kita menggunakan faktor skala 1:1000. Artinya, setiap 1 meter di taman akan direpresentasikan sebagai 1 milimeter di peta.
Dengan menerapkan dilatasi dengan faktor skala 1/1000 terhadap titik pusat (misalnya, pusat taman), kita akan mendapatkan representasi taman di peta dengan panjang 10 cm dan lebar 5 cm. Setiap detail dalam taman, seperti jalan setapak, pohon, dan bangku, juga akan diperkecil dengan faktor skala yang sama, mempertahankan proporsi relatifnya.
Keterkaitan Dilatasi dengan Pembesaran atau Pengecilan Gambar
Dilatasi secara langsung berkaitan dengan pembesaran dan pengecilan gambar. Pembesaran gambar adalah dilatasi dengan faktor skala lebih besar dari 1, sementara pengecilan gambar adalah dilatasi dengan faktor skala antara 0 dan 1. Proses ini mempertahankan rasio aspek gambar asli, sehingga gambar yang dihasilkan tetap proporsional, meskipun ukurannya berubah.
Penerapan Dilatasi dalam Teknologi Fotografi dan Desain Grafis
Dalam perangkat lunak pengolah gambar, fungsi “zoom” atau “resize” menggunakan prinsip dilatasi. Ketika kita memperbesar atau memperkecil foto, software tersebut melakukan transformasi dilatasi terhadap gambar digital, mengubah ukuran piksel-piksel penyusun gambar tanpa mengubah bentuknya. Perbedaannya terletak pada bagaimana software tersebut menangani informasi piksel untuk menjaga kualitas gambar, misalnya dengan interpolasi untuk pembesaran, atau pengurangan detail untuk pengecilan.
Kesimpulan Akhir: Contoh Soal Dilatasi
Setelah mempelajari berbagai contoh soal dilatasi dan penyelesaiannya, diharapkan pemahaman Anda tentang transformasi geometri ini semakin mantap. Dilatasi, yang tampak sederhana, memiliki aplikasi luas dalam berbagai bidang, mulai dari arsitektur hingga desain grafis. Kemampuan untuk menganalisis dan menyelesaikan soal dilatasi akan sangat bermanfaat dalam memahami konsep-konsep geometri yang lebih kompleks di masa mendatang. Teruslah berlatih dan eksplorasi dunia geometri yang menarik ini!