- Pengertian Bentuk Akar
- Operasi pada Bentuk Akar
-
Rasionalisasi Bentuk Akar: Contoh Bentuk Akar
- Pengertian Rasionalisasi Bentuk Akar
- Contoh Rasionalisasi Bentuk Akar dengan Penyebut Bentuk Akar Tunggal, Contoh bentuk akar
- Contoh Rasionalisasi Bentuk Akar dengan Penyebut Berupa Penjumlahan atau Pengurangan Bentuk Akar
- Langkah-langkah Rasionalisasi Bentuk Akar
- Contoh Soal Menantang Rasionalisasi Bentuk Akar
- Penerapan Bentuk Akar dalam Kehidupan Sehari-hari
- Persamaan dan Pertidaksamaan Bentuk Akar
- Ringkasan Penutup
Contoh bentuk akar, merupakan konsep matematika yang mungkin tampak rumit pada awalnya, namun sebenarnya sangat menarik dan bermanfaat. Bentuk akar, atau akar kuadrat, merupakan kebalikan dari operasi kuadrat (pangkat dua). Memahami bentuk akar membuka pintu untuk menjelajahi berbagai aplikasi dalam geometri, fisika, dan bahkan kehidupan sehari-hari. Mari kita mulai petualangan kita dalam memahami dunia bilangan irasional ini!
Dalam panduan ini, kita akan membahas definisi bentuk akar, operasi-operasi yang dapat dilakukan padanya, teknik rasionalisasi, serta penerapannya dalam berbagai konteks. Kita akan memperkuat pemahaman kita melalui contoh soal dan penyelesaian langkah demi langkah, sehingga konsep yang awalnya terlihat membingungkan akan menjadi jelas dan mudah dipahami.
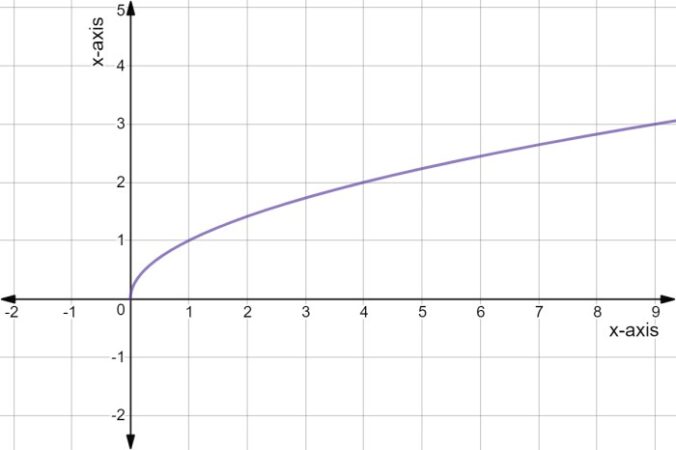
Pengertian Bentuk Akar

Bentuk akar merupakan suatu konsep dalam matematika yang berkaitan dengan representasi bilangan irasional. Secara sederhana, bentuk akar adalah cara penulisan bilangan yang pangkatnya merupakan pecahan, khususnya pecahan dengan pembilang 1. Pemahaman tentang bentuk akar penting dalam berbagai perhitungan matematika, khususnya aljabar dan geometri.
Definisi Matematis Bentuk Akar
Secara matematis, bentuk akar didefinisikan sebagai √a, dimana ‘a’ adalah bilangan real tak negatif, dan √ merupakan simbol akar kuadrat. Akar kuadrat dari ‘a’ adalah bilangan ‘x’ sedemikian sehingga x² = a. Konsep ini dapat diperluas ke akar pangkat n, ditulis sebagai ⁿ√a, yang berarti bilangan ‘x’ sedemikian sehingga xⁿ = a. Bentuk akar berkaitan erat dengan pangkat pecahan, karena √a dapat ditulis sebagai a 1/2, dan ⁿ√a dapat ditulis sebagai a 1/n.
Contoh Bentuk Akar Berbagai Jenis Bilangan
Bentuk akar dapat melibatkan berbagai jenis bilangan. Berikut beberapa contoh:
- Bilangan bulat: √9 = 3 (akar kuadrat dari 9 adalah 3 karena 3² = 9)
- Bilangan desimal: √2.25 = 1.5 (akar kuadrat dari 2.25 adalah 1.5 karena 1.5² = 2.25)
- Bilangan pecahan: √(9/16) = 3/4 (akar kuadrat dari 9/16 adalah 3/4 karena (3/4)² = 9/16)
- Bilangan irasional: √2 ≈ 1.414 (akar kuadrat dari 2 adalah bilangan irasional, yang artinya tidak dapat dinyatakan sebagai pecahan sederhana)
Perbedaan Bentuk Akar dan Bilangan Rasional
Perbedaan utama antara bentuk akar dan bilangan rasional terletak pada kemampuannya untuk dinyatakan sebagai pecahan sederhana. Bilangan rasional dapat dinyatakan sebagai rasio dua bilangan bulat (a/b, dengan b ≠ 0). Bentuk akar, khususnya akar dari bilangan bukan kuadrat sempurna, menghasilkan bilangan irasional yang tidak dapat dinyatakan sebagai pecahan sederhana. Contohnya, √2 adalah bilangan irasional, sedangkan 3/4 adalah bilangan rasional.
Karakteristik Utama Bentuk Akar
Karakteristik utama yang membedakan bentuk akar dari jenis bilangan lain adalah sifat irasionalitasnya. Banyak bentuk akar mewakili bilangan irasional, yang memiliki desimal tak berulang dan tak berakhir. Selain itu, operasi pada bentuk akar seringkali menghasilkan bentuk akar baru, dan penyederhanaan bentuk akar memerlukan pemahaman tentang faktorisasi dan sifat-sifat akar.
Contoh Soal Identifikasi Bentuk Akar dalam Persamaan
Perhatikan persamaan berikut: x²
-5 = 0. Untuk menyelesaikan persamaan ini, kita perlu mengisolasi x dan menemukan akar kuadrat dari 5. Oleh karena itu, solusi persamaan tersebut adalah x = ±√5. Dalam persamaan ini, √5 merupakan bentuk akar yang mewakili solusi persamaan kuadrat tersebut.
Operasi pada Bentuk Akar
Bentuk akar, atau disebut juga dengan radikal, merupakan representasi matematis dari suatu bilangan yang dipangkatkan dengan pecahan. Memahami operasi pada bentuk akar sangat penting dalam berbagai bidang matematika, termasuk aljabar dan kalkulus. Operasi-operasi dasar seperti penjumlahan, pengurangan, perkalian, dan pembagian pada bentuk akar memiliki aturan khusus yang perlu dipahami untuk mendapatkan hasil yang tepat dan sederhana.
Berikut ini akan dijelaskan operasi-operasi tersebut beserta contoh dan cara penyederhanaannya.
Operasi Aritmatika pada Bentuk Akar
Tabel berikut merangkum operasi penjumlahan, pengurangan, perkalian, dan pembagian pada bentuk akar. Perlu diingat bahwa operasi penjumlahan dan pengurangan hanya dapat dilakukan jika bentuk akarnya sama (memiliki angka di dalam akar yang sama).
| Operasi | Rumus | Contoh | Penjelasan |
|---|---|---|---|
| Penjumlahan | a√b + c√b = (a+c)√b | 2√3 + 5√3 = 7√3 | Jumlahkan koefisien jika bentuk akarnya sama. |
| Pengurangan | a√b – c√b = (a-c)√b | 8√5 – 3√5 = 5√5 | Kurangkan koefisien jika bentuk akarnya sama. |
| Perkalian | (a√b)(c√d) = ac√(bd) | (2√3)(4√5) = 8√15 | Kalikan koefisien dan angka di dalam akar secara terpisah. |
| Pembagian | (a√b) / (c√d) = (a/c)√(b/d) | (6√12) / (2√3) = 3√4 = 6 | Bagi koefisien dan angka di dalam akar secara terpisah. |
Contoh Perhitungan dan Penyederhanaan Bentuk Akar
Berikut ini contoh perhitungan untuk masing-masing operasi dan penyederhanaannya menggunakan faktorisasi prima:
Contoh Penjumlahan: 3√2 + 5√2 = 8√2 (bentuk sudah sederhana)
Contoh Pengurangan: 7√5 – 2√5 = 5√5 (bentuk sudah sederhana)
Contoh Perkalian: 2√6 x 3√2 = 6√12 = 6√(2² x 3) = 6 x 2√3 = 12√3
Langkah-langkah penyederhanaan: Perkalian koefisien (2×3=6), perkalian angka dalam akar (6×2=12), kemudian faktorkan 12 menjadi 2² x 3. Keluarkan 2 dari dalam akar.
Contoh Pembagian: 10√18 / 2√2 = 5√9 = 5 x 3 = 15
Langkah-langkah penyederhanaan: Pembagian koefisien (10/2=5), pembagian angka dalam akar (18/2=9), kemudian sederhanakan √9 menjadi 3.
Penyederhanaan Bentuk Akar dengan Faktorisasi Prima
Faktorisasi prima merupakan metode efektif untuk menyederhanakan bentuk akar. Dengan memecah angka di dalam akar menjadi faktor-faktor prima, kita dapat menemukan faktor-faktor yang membentuk kuadrat sempurna dan mengeluarkannya dari dalam akar.
Contoh: Sederhanakan √72. Faktorisasi prima dari 72 adalah 2³ x 3². Maka √72 = √(2³ x 3²) = √(2² x 2 x 3²) = 2 x 3√2 = 6√2
Contoh Soal Kombinasi Operasi Bentuk Akar
Hitunglah nilai dari (2√3 + √12) x √3 – 5√6.
Penyelesaian:
- Sederhanakan √12 = √(2² x 3) = 2√3
- Substitusikan: (2√3 + 2√3) x √3 – 5√6 = (4√3) x √3 – 5√6
- Perkalian: 4 x 3 – 5√6 = 12 – 5√6
Jadi, nilai dari (2√3 + √12) x √3 – 5√6 adalah 12 – 5√6.
Rasionalisasi Bentuk Akar: Contoh Bentuk Akar

Rasionalisasi bentuk akar merupakan teknik aljabar yang digunakan untuk menyederhanakan bentuk akar, khususnya yang terdapat pada penyebut suatu pecahan. Tujuannya adalah untuk menghilangkan bentuk akar dari penyebut, sehingga pecahan tersebut menjadi lebih sederhana dan mudah dioperasikan. Proses ini sangat berguna dalam berbagai perhitungan matematika, terutama dalam kalkulus dan aljabar.
Pengertian Rasionalisasi Bentuk Akar
Rasionalisasi bentuk akar adalah proses menghilangkan bentuk akar dari penyebut suatu pecahan dengan cara mengalikan pembilang dan penyebut dengan bentuk akar yang tepat. Bentuk akar yang tepat ini dipilih sedemikian rupa sehingga hasil perkalian pada penyebut menghasilkan bilangan rasional (bilangan bulat atau pecahan biasa).
Contoh Rasionalisasi Bentuk Akar dengan Penyebut Bentuk Akar Tunggal, Contoh bentuk akar
Misalnya, kita ingin merasionalkan pecahan 2⁄ √3. Untuk menghilangkan √3 pada penyebut, kita kalikan pembilang dan penyebut dengan √
3. Hasilnya adalah:
2⁄ √3 x √3⁄ √3 = 2√3⁄ 3
Sekarang, penyebutnya sudah menjadi bilangan rasional, yaitu 3.
Contoh Rasionalisasi Bentuk Akar dengan Penyebut Berupa Penjumlahan atau Pengurangan Bentuk Akar
Jika penyebutnya berupa penjumlahan atau pengurangan bentuk akar, kita perlu menggunakan konsep perkalian selisih dua kuadrat. Misalnya, kita ingin merasionalkan 1⁄ (√5 + √2). Kita kalikan pembilang dan penyebut dengan bentuk sekawannya, yaitu (√5 – √2):
1⁄ (√5 + √2) x (√5 – √2)⁄ (√5 – √2) = (√5 – √2)⁄ (5 – 2) = (√5 – √2)⁄ 3
Perhatikan bahwa (√5 + √2)(√5 – √2) = 5 – 2 = 3, sehingga bentuk akar pada penyebut hilang.
Langkah-langkah Rasionalisasi Bentuk Akar
- Identifikasi bentuk akar yang berada pada penyebut.
- Jika penyebut berupa bentuk akar tunggal, kalikan pembilang dan penyebut dengan bentuk akar tersebut.
- Jika penyebut berupa penjumlahan atau pengurangan bentuk akar, kalikan pembilang dan penyebut dengan bentuk sekawannya.
- Sederhanakan hasil perkalian.
Contoh Soal Menantang Rasionalisasi Bentuk Akar
Rasionalkan bentuk akar berikut: (√6 + √2)⁄ (√3 – √2) . Soal ini membutuhkan pemahaman mendalam karena melibatkan dua bentuk akar baik pada pembilang maupun penyebut. Penyelesaiannya membutuhkan dua tahap rasionalisasi, pertama dengan mengalikan bentuk sekawan pada penyebut, kemudian menyederhanakan hasil dan jika perlu, melakukan rasionalisasi kembali.
Langkah penyelesaian: Pertama rasionalkan penyebut dengan mengalikan pembilang dan penyebut dengan (√3 + √2). Kemudian, sederhanakan hasil dan rasionalkan kembali jika perlu. Hasil akhirnya akan berupa bentuk yang lebih sederhana tanpa akar pada penyebut.
Penerapan Bentuk Akar dalam Kehidupan Sehari-hari
Bentuk akar, meskipun mungkin terlihat rumit dalam pembelajaran matematika, ternyata memiliki penerapan yang luas dan praktis dalam kehidupan sehari-hari. Kemampuan untuk menghitung dan memahami bentuk akar sangat membantu dalam berbagai bidang, mulai dari perhitungan sederhana hingga penyelesaian masalah yang lebih kompleks dalam geometri, fisika, dan bahkan dalam aktivitas sehari-hari yang mungkin tidak kita sadari.
Penerapan Bentuk Akar dalam Geometri
Bentuk akar seringkali muncul dalam perhitungan geometri. Teorema Pythagoras, misalnya, yang menyatakan bahwa kuadrat sisi miring segitiga siku-siku sama dengan jumlah kuadrat kedua sisi lainnya, seringkali menghasilkan solusi yang melibatkan bentuk akar. Kita dapat menggunakannya untuk menghitung panjang diagonal suatu persegi atau panjang sisi miring segitiga siku-siku.
- Menghitung Panjang Diagonal Persegi: Jika sebuah persegi memiliki sisi sepanjang 5 cm, maka panjang diagonalnya dapat dihitung dengan menggunakan rumus √(5² + 5²) = √50 = 5√2 cm.
- Menghitung Luas Segitiga: Untuk menghitung luas segitiga jika diketahui alas dan tinggi, terkadang kita akan menemukan bentuk akar dalam perhitungan. Misalnya, jika alas segitiga adalah 6 cm dan tingginya 4 cm, maka luasnya adalah ½
– 6
– 4 = 12 cm². Namun, jika kita hanya mengetahui dua sisi dan sudut di antaranya, perhitungan luas akan melibatkan rumus yang menghasilkan bentuk akar.
Penerapan Bentuk Akar dalam Fisika
Dalam fisika, bentuk akar sering muncul dalam rumus yang berkaitan dengan kecepatan, jarak, dan percepatan. Penggunaan bentuk akar dalam fisika membantu dalam perhitungan yang akurat dan presisi.
- Menghitung Kecepatan: Rumus kecepatan yang melibatkan percepatan dan jarak seringkali melibatkan bentuk akar. Misalnya, jika suatu benda bergerak dengan percepatan konstan ‘a’ dari keadaan diam dan menempuh jarak ‘s’, maka kecepatan akhirnya (v) dapat dihitung dengan rumus v = √(2as).
- Menghitung Jarak: Sebaliknya, jika kita mengetahui kecepatan awal, kecepatan akhir, dan percepatan, kita dapat menghitung jarak yang ditempuh menggunakan rumus yang melibatkan bentuk akar.
Penerapan Bentuk Akar dalam Perhitungan Luas dan Volume Bangun Ruang
Perhitungan luas permukaan dan volume bangun ruang tertentu, seperti kerucut dan bola, seringkali melibatkan bentuk akar dalam rumusnya. Ketepatan perhitungan ini penting dalam berbagai aplikasi, mulai dari desain bangunan hingga pembuatan berbagai produk.
- Luas Permukaan Kerucut: Rumus luas permukaan kerucut melibatkan πr√(r²+h²), di mana r adalah jari-jari alas dan h adalah tinggi kerucut. Ini menunjukkan bahwa bentuk akar diperlukan untuk perhitungan yang akurat.
- Volume Bola: Rumus volume bola (4/3)πr³ tidak secara langsung melibatkan bentuk akar, namun perhitungan jari-jari bola dari volume yang diketahui, atau sebaliknya, seringkali memerlukan manipulasi aljabar yang menghasilkan bentuk akar.
Contoh Kasus Sederhana Penerapan Bentuk Akar
Bayangkan Anda ingin memasang kabel dari puncak tiang listrik setinggi 12 meter ke titik di tanah yang berjarak 5 meter dari pangkal tiang. Panjang kabel yang dibutuhkan dapat dihitung menggunakan Teorema Pythagoras: √(12² + 5²) = √169 = 13 meter.
Penggunaan Bentuk Akar dalam Skala dan Perbandingan
Bentuk akar digunakan dalam berbagai aplikasi yang melibatkan skala dan perbandingan, seperti dalam pembuatan peta atau model. Pemahaman tentang bentuk akar membantu dalam melakukan konversi skala dengan akurat dan memastikan proporsionalitas yang tepat.
- Peta: Skala pada peta seringkali dinyatakan sebagai perbandingan, misalnya 1:1000. Ini berarti bahwa 1 cm pada peta mewakili 1000 cm atau 10 meter di dunia nyata. Perhitungan jarak sebenarnya dari jarak pada peta akan melibatkan bentuk akar jika kita menghitung jarak yang tidak lurus.
- Model: Pembuatan model bangunan atau objek lainnya juga melibatkan skala dan perbandingan. Perhitungan ukuran model yang proporsional dengan objek aslinya akan memerlukan pemahaman dan penggunaan bentuk akar.
Persamaan dan Pertidaksamaan Bentuk Akar
Persamaan dan pertidaksamaan yang melibatkan bentuk akar merupakan bagian penting dalam aljabar. Memahami cara menyelesaikannya membutuhkan pemahaman yang kuat tentang sifat-sifat akar dan manipulasi aljabar. Ketelitian dalam setiap langkah sangat krusial untuk menghindari kesalahan dan mendapatkan solusi yang tepat. Berikut penjelasan lebih lanjut mengenai penyelesaian persamaan dan pertidaksamaan bentuk akar.
Metode Penyelesaian Persamaan dan Pertidaksamaan Bentuk Akar
Penyelesaian persamaan dan pertidaksamaan bentuk akar umumnya melibatkan beberapa langkah kunci. Langkah pertama adalah mengisolasi bentuk akar agar dapat dikuadratkan untuk menghilangkan tanda akar. Namun, perlu diingat bahwa mengkuadratkan kedua ruas persamaan dapat menghasilkan akar-akar asing, sehingga verifikasi solusi sangat penting. Untuk pertidaksamaan, setelah mengisolasi bentuk akar dan mengkuadratkan, kita perlu memperhatikan tanda ketidaksamaan dan domain dari variabel agar solusi yang diperoleh valid.
Contoh Soal Persamaan Bentuk Akar
Mari kita selesaikan persamaan berikut: √(x + 2) = x.
- Kuadratkan kedua ruas: (√(x + 2))² = x² ⇒ x + 2 = x²
- Susun ulang persamaan menjadi persamaan kuadrat: x²
x – 2 = 0
- Faktorkan persamaan kuadrat: (x – 2)(x + 1) = 0
- Solusi persamaan kuadrat adalah x = 2 atau x = -1
- Verifikasi solusi:
- Untuk x = 2: √(2 + 2) = √4 = 2. Solusi valid.
- Untuk x = -1: √(-1 + 2) = √1 = 1 ≠ -1. Solusi tidak valid.
- Jadi, solusi persamaan adalah x = 2.
Contoh Soal Pertidaksamaan Bentuk Akar
Mari kita selesaikan pertidaksamaan berikut: √(x – 1) ≤ 2.
- Kuadratkan kedua ruas: (√(x – 1))² ≤ 2² ⇒ x – 1 ≤ 4
- Selesaikan pertidaksamaan: x ≤ 5
- Perhatikan domain dari √(x – 1): x – 1 ≥ 0 ⇒ x ≥ 1
- Gabungkan kedua kondisi: x ≥ 1 dan x ≤ 5
- Jadi, solusi pertidaksamaan adalah 1 ≤ x ≤ 5.
Potensi Kesalahan Umum dalam Menyelesaikan Persamaan dan Pertidaksamaan Bentuk Akar
Kesalahan umum yang sering terjadi adalah melupakan verifikasi solusi setelah mengkuadratkan kedua ruas persamaan. Mengkuadratkan dapat menghasilkan akar-akar asing yang tidak memenuhi persamaan atau pertidaksamaan asli. Selain itu, mengabaikan domain dari variabel dalam akar juga dapat menghasilkan solusi yang tidak valid. Kesalahan lain yang mungkin terjadi adalah kesalahan dalam manipulasi aljabar saat menyederhanakan persamaan atau pertidaksamaan.
Contoh Soal Gabungan Persamaan dan Pertidaksamaan Bentuk Akar
Tentukan nilai x yang memenuhi √(x + 3) + 1 = x dan x ≥ 0.
- Susun ulang persamaan: √(x + 3) = x – 1
- Kuadratkan kedua ruas: x + 3 = (x – 1)² ⇒ x + 3 = x² – 2x + 1
- Susun ulang menjadi persamaan kuadrat: x²
3x – 2 = 0
- Selesaikan persamaan kuadrat (misalnya dengan rumus kuadrat): x = (3 ± √17)/2
- Karena x ≥ 0, maka hanya x = (3 + √17)/2 yang memenuhi.
- Verifikasi solusi: Substitusikan x = (3 + √17)/2 ke persamaan awal untuk memastikan kesetaraan.
Ringkasan Penutup
Dengan memahami konsep bentuk akar dan berbagai aplikasinya, kita telah membuka jalan menuju pemahaman yang lebih dalam tentang matematika. Mulai dari operasi dasar hingga rasionalisasi dan penyelesaian persamaan, kemampuan untuk memanipulasi bentuk akar memberikan alat yang ampuh untuk memecahkan berbagai masalah, baik dalam konteks akademis maupun dunia nyata. Semoga panduan ini membantu dalam menguasai konsep penting ini!