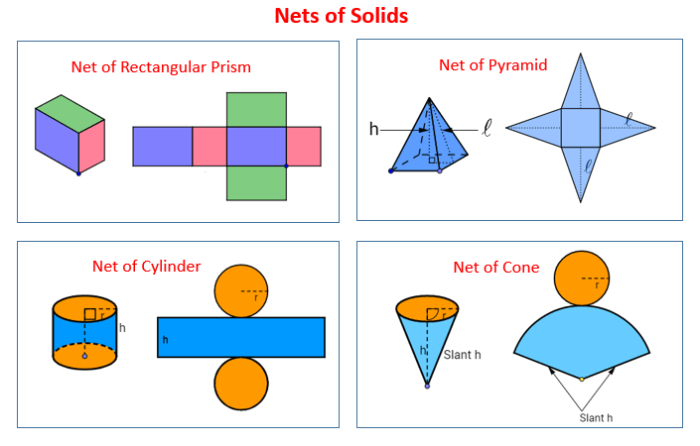
Bentuk jaring jaring kubus – Bentuk jaring-jaring kubus merupakan representasi dua dimensi dari bangun ruang tiga dimensi, kubus. Memahami berbagai bentuk jaring-jaring kubus sangat penting, tidak hanya untuk pelajaran geometri, tetapi juga untuk aplikasi praktis dalam berbagai bidang, seperti desain kemasan dan pembuatan kerajinan. Dari sekian banyak kemungkinan bentuk, mengenali karakteristik dan sifat-sifatnya akan membantu kita memahami bagaimana sebuah bangun datar dapat diubah menjadi bangun ruang yang kokoh.
Artikel ini akan membahas secara detail berbagai bentuk jaring-jaring kubus, jumlah kemungkinan bentuknya, sifat-sifatnya, aplikasinya dalam kehidupan sehari-hari, serta langkah-langkah membuatnya. Dengan pemahaman yang komprehensif, diharapkan pembaca dapat dengan mudah membayangkan dan bahkan menciptakan kubus dari jaring-jaringnya sendiri.
Pengertian Jaring-Jaring Kubus
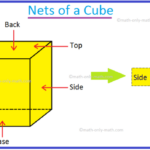
Jaring-jaring kubus merupakan susunan bangun datar berupa enam persegi yang jika dilipat menurut garis-garis lipatannya akan membentuk bangun ruang kubus. Mempelajari jaring-jaring kubus penting untuk memahami bagaimana bangun ruang tiga dimensi dapat diuraikan menjadi bangun datar dua dimensi dan sebaliknya. Pemahaman ini berguna dalam berbagai bidang, seperti desain kemasan, arsitektur, dan matematika.
Secara sederhana, jaring-jaring kubus adalah pola dua dimensi yang dapat dilipat untuk membentuk kubus tiga dimensi. Setiap persegi pada jaring-jaring mewakili sisi kubus, dan garis-garis yang menghubungkan persegi tersebut menunjukkan tempat lipatan akan dibuat. Terdapat berbagai macam bentuk jaring-jaring kubus, meskipun semuanya terdiri dari enam persegi.
Contoh Bentuk Jaring-Jaring Kubus
Berikut adalah tiga contoh bentuk jaring-jaring kubus yang berbeda:
- Jaring-jaring kubus berbentuk seperti huruf “T” atau “+”. Ini adalah salah satu bentuk jaring-jaring kubus yang paling umum.
- Jaring-jaring kubus berbentuk seperti garis lurus dengan empat persegi berjajar dan dua persegi yang menempel di sisi-sisi yang berlawanan.
- Jaring-jaring kubus berbentuk seperti tangga, dengan tiga persegi berjajar secara vertikal dan tiga persegi lainnya menempel di sisi-sisi yang berlawanan.
Tabel Bentuk Jaring-Jaring Kubus
Tabel berikut merangkum beberapa bentuk jaring-jaring kubus beserta karakteristiknya:
| Nama Bentuk | Jumlah Persegi | Deskripsi Singkat |
|---|---|---|
| Bentuk T/Plus | 6 | Empat persegi berjajar membentuk garis vertikal, dengan dua persegi lainnya menempel di sisi-sisi yang berlawanan. |
| Bentuk Garis Lurus | 6 | Empat persegi berjajar secara horizontal, dengan dua persegi lainnya menempel di sisi-sisi yang berlawanan. |
| Bentuk Tangga | 6 | Tiga persegi berjajar secara vertikal, dengan tiga persegi lainnya menempel di sisi-sisi yang berlawanan. |
Karakteristik Umum Jaring-Jaring Kubus
Semua jaring-jaring kubus memiliki karakteristik umum, yaitu:
- Terdiri dari enam persegi.
- Setiap persegi memiliki sisi yang sama panjang.
- Saat dilipat, setiap sisi persegi akan bertemu dengan tepat satu sisi persegi lainnya, membentuk enam sisi kubus.
- Tidak ada dua persegi yang saling tumpang tindih saat dilipat.
Ilustrasi Detail Jaring-Jaring Kubus
Bayangkan sebuah jaring-jaring kubus berbentuk “T”. Persegi di bagian atas “T” akan menjadi bagian atas kubus. Dua persegi yang berdampingan di bagian tengah “T” akan menjadi sisi-sisi kubus yang bersebelahan. Dua persegi yang berada di bagian bawah “T” akan menjadi sisi-sisi kubus yang bersebelahan dan saling berhadapan dengan persegi bagian atas. Persegi terakhir, yang menempel pada salah satu persegi bagian bawah, akan menjadi sisi kubus yang berlawanan dengan persegi atas.
Saat dilipat, setiap sisi persegi akan terhubung dengan sisi persegi lainnya di sepanjang garis-garis lipatan, membentuk enam sisi kubus yang terhubung sempurna.
Jumlah Jaring-Jaring Kubus
Kubus, bangun ruang tiga dimensi yang familiar, ternyata memiliki beragam kemungkinan bentuk jaring-jaring. Menentukan jumlah total kemungkinan bentuk jaring-jaring kubus membutuhkan pendekatan sistematis. Pemahaman tentang jumlah ini penting dalam memahami berbagai cara untuk membangun kubus dari bentuk dua dimensi dan membantu dalam pemecahan masalah geometri.
Terdapat sebelas kemungkinan bentuk jaring-jaring kubus yang berbeda. Metode penentuan jumlah ini melibatkan menganalisis semua kemungkinan pengaturan enam persegi yang saling bersebelahan, dengan memperhatikan batasan agar dapat membentuk kubus ketika dilipat. Prosesnya cukup rumit jika dilakukan secara manual, tetapi dengan pendekatan sistematis, kita dapat memastikan tidak ada bentuk yang terlewatkan.
Langkah-Langkah Penentuan Jumlah Jaring-Jaring Kubus
Menentukan jumlah jaring-jaring kubus secara sistematis dapat dilakukan dengan beberapa langkah. Pertama, kita mulai dengan satu persegi sebagai dasar. Kemudian, kita tambahkan persegi-persegi lain secara bertahap, selalu memperhatikan kondisi agar persegi-persegi tersebut dapat membentuk kubus ketika dilipat. Dengan metode ini, kita dapat menghindari penghitungan berulang dan memastikan semua kemungkinan bentuk tercakup.
- Mulai dengan satu persegi sebagai pusat.
- Tambahkan persegi-persegi lain di sekeliling persegi pertama, dengan memperhatikan aturan bahwa sisi-sisi yang bersebelahan harus saling terhubung.
- Ulangi langkah kedua hingga enam persegi terpasang. Pastikan setiap konfigurasi dapat membentuk kubus jika dilipat.
- Eliminasi konfigurasi yang menghasilkan bentuk yang sama melalui rotasi atau refleksi.
- Hasil akhir akan menunjukkan sebelas konfigurasi unik yang mewakili semua kemungkinan jaring-jaring kubus.
Visualisasi Jaring-Jaring Kubus
Berikut gambaran sederhana sebelas jaring-jaring kubus. Bayangkan setiap persegi sebagai sisi kubus. Perhatikan bagaimana setiap konfigurasi dapat dilipat untuk membentuk kubus yang utuh. Meskipun tampak sederhana, proses menemukan semua konfigurasi ini memerlukan ketelitian dan pendekatan sistematis.
Visualisasikanlah sebelas bentuk ini: Bayangkan enam persegi disusun dalam berbagai konfigurasi, seperti misalnya: tiga persegi berjajar, dengan dua persegi di atas dan satu persegi di bawahnya; atau empat persegi berjajar, dengan satu persegi di atas dan satu di bawahnya; dan berbagai variasi lainnya yang tetap dapat membentuk kubus saat dilipat.
Perbandingan Dua Jaring-Jaring Kubus
Mari bandingkan dua jaring-jaring kubus yang berbeda sebagai contoh. Misalnya, perhatikan konfigurasi empat persegi berjajar horizontal dengan satu persegi di atas dan satu di bawahnya. Bandingkan dengan konfigurasi tiga persegi vertikal dengan dua persegi di samping dan satu persegi di bawah. Keduanya memiliki enam persegi, dan keduanya dapat membentuk kubus ketika dilipat. Perbedaannya terletak pada susunan spasial persegi-persegi tersebut.
Kesamaannya adalah keduanya memenuhi syarat sebagai jaring-jaring kubus yang valid.
Sifat-Sifat Jaring-Jaring Kubus
Memahami sifat-sifat jaring-jaring kubus sangat penting untuk membangun kubus yang benar dan utuh. Sifat-sifat ini menentukan bagaimana bentuk dua dimensi ini dapat dilipat menjadi bentuk tiga dimensi yang dikenal sebagai kubus. Kemampuan untuk mengenali dan menerapkan sifat-sifat ini sangat berguna, baik dalam konteks pembelajaran geometri maupun dalam aplikasi praktis kehidupan sehari-hari.
Jumlah Persegi
Jaring-jaring kubus selalu terdiri dari enam persegi identik. Ini merupakan sifat fundamental yang membedakannya dari jaring-jaring bangun ruang lainnya. Tidak ada jaring-jaring kubus yang memiliki kurang atau lebih dari enam persegi. Keberadaan keenam persegi ini mencerminkan enam sisi kubus yang sama bentuk dan ukurannya. Contoh penerapannya terlihat pada kemasan makanan berbentuk kubus, dimana keenam sisinya digunakan untuk menampilkan informasi produk.
Susunan Persegi
Keenam persegi pada jaring-jaring kubus tersusun sedemikian rupa sehingga setiap persegi berbatasan dengan minimal satu persegi lainnya. Tidak ada persegi yang terisolasi atau terpisah dari persegi lainnya. Susunan ini memastikan bahwa ketika jaring-jaring dilipat, keenam sisi kubus akan terhubung dengan sempurna. Bayangkan sebuah jaring-jaring yang berbentuk seperti salib, dimana persegi tengahnya dikelilingi oleh empat persegi lainnya, dan dua persegi tersisa di sisi atas dan bawah.
Ini adalah contoh susunan yang tepat.
Kecocokan Sisi
Setiap sisi persegi pada jaring-jaring kubus harus memiliki sisi yang berpasangan dan identik untuk dapat membentuk kubus. Hal ini memastikan bahwa ketika dilipat, semua sisi akan bertemu dengan sempurna dan membentuk enam sisi kubus yang beraturan. Jika ada ketidakcocokan pada ukuran atau bentuk sisi persegi, maka kubus yang dihasilkan akan tidak sempurna atau bahkan tidak dapat terbentuk. Misalnya, jika salah satu persegi lebih besar dari yang lain, maka akan terjadi celah atau tumpang tindih saat dilipat.
Kemungkinan Bentuk Jaring-Jaring
Meskipun jumlah dan bentuk persegi selalu sama, terdapat beberapa kemungkinan susunan atau konfigurasi jaring-jaring kubus. Tidak semua susunan enam persegi akan membentuk kubus. Hanya susunan-susunan tertentu yang memungkinkan lipatan membentuk bangun ruang kubus yang sempurna. Terdapat sebelas kemungkinan konfigurasi jaring-jaring kubus yang berbeda, masing-masing memiliki susunan persegi yang unik namun tetap memenuhi syarat keenam sifat jaring-jaring kubus.
Implikasi Terhadap Konstruksi Kubus
Sifat-sifat jaring-jaring kubus secara langsung mempengaruhi proses konstruksi kubus. Pemahaman tentang jumlah, susunan, dan kecocokan sisi persegi sangat krusial untuk memastikan keberhasilan dalam membentuk kubus. Jika salah satu sifat tidak dipenuhi, maka proses pelipatan akan mengalami kendala dan kubus yang dihasilkan akan cacat atau tidak terbentuk sama sekali. Sebagai contoh, jika kita menggunakan jaring-jaring yang salah, kita tidak akan bisa membentuk kubus yang sempurna, dan akan terlihat celah atau lipatan yang tidak rata.
Aplikasi Jaring-Jaring Kubus
Jaring-jaring kubus, lebih dari sekadar gambar geometris, memiliki aplikasi praktis yang luas di berbagai bidang. Pemahaman tentang jaring-jaring ini memungkinkan kita untuk merancang dan membuat berbagai objek tiga dimensi dengan efisiensi dan presisi. Berikut beberapa contoh penerapannya.
Aplikasi Jaring-Jaring Kubus dalam Berbagai Bidang
Kegunaan jaring-jaring kubus melampaui pembelajaran geometri dasar. Penerapannya dapat ditemukan dalam desain kemasan, konstruksi, dan bahkan dalam dunia seni dan kerajinan. Berikut beberapa contoh spesifiknya:
- Kemasan Produk: Banyak produk dikemas dalam kotak berbentuk kubus, seperti makanan ringan, mainan, atau perangkat elektronik kecil. Desain jaring-jaring kubus memastikan efisiensi penggunaan material dan kemudahan perakitan. Contohnya, kotak kemasan susu kotak yang kita jumpai sehari-hari.
- Konstruksi Bangunan: Meskipun tidak secara langsung terlihat, prinsip jaring-jaring kubus dapat diterapkan dalam perencanaan dan konstruksi bangunan, terutama dalam hal perhitungan volume dan efisiensi material. Misalnya, dalam perencanaan struktur balok penyangga yang membentuk kubus tiga dimensi.
- Seni dan Kerajinan: Jaring-jaring kubus dapat menjadi dasar pembuatan berbagai karya seni tiga dimensi. Contohnya, pembuatan kotak perhiasan, model bangunan sederhana, atau bahkan patung abstrak dengan struktur kubus sebagai elemen utamanya.
Manfaat Jaring-Jaring Kubus dalam Desain dan Konstruksi
Penggunaan jaring-jaring kubus dalam desain dan konstruksi memungkinkan perencanaan yang lebih akurat dan efisien. Dengan memahami bagaimana sebuah kubus dapat diuraikan menjadi jaring-jaring dua dimensi, kita dapat mengoptimalkan penggunaan material, mengurangi limbah, dan mempermudah proses perakitan. Hal ini berujung pada penghematan biaya dan waktu.
Potensi Pengembangan Aplikasi Jaring-Jaring Kubus di Masa Depan
Dengan perkembangan teknologi seperti pencetakan 3D dan desain berbantuan komputer (CAD), potensi aplikasi jaring-jaring kubus semakin luas. Di masa depan, kita dapat mengharapkan desain yang lebih kompleks dan inovatif berdasarkan prinsip jaring-jaring kubus. Misalnya, dalam pengembangan struktur bangunan yang lebih kuat dan ringan, atau dalam pembuatan kemasan yang ramah lingkungan dan mudah didaur ulang.
Langkah-Langkah Membuat Kotak Kemasan Sederhana
Membuat kotak kemasan sederhana dengan prinsip jaring-jaring kubus relatif mudah. Berikut langkah-langkahnya:
- Desain Jaring-Jaring: Gambarlah jaring-jaring kubus pada kertas sesuai ukuran yang diinginkan. Pastikan setiap sisi memiliki ukuran yang sama.
- Potong Kertas: Potong kertas sesuai dengan bentuk jaring-jaring yang telah digambar.
- Lipat Kertas: Lipat kertas di sepanjang garis yang telah digambar, sehingga membentuk bentuk kubus.
- Rekatkan: Gunakan lem atau selotip untuk merekatkan sisi-sisi kubus agar terpasang dengan kuat.
Membuat Jaring-Jaring Kubus
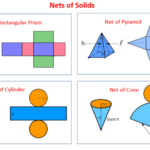
Membuat jaring-jaring kubus merupakan aktivitas yang menyenangkan dan sekaligus edukatif, baik untuk anak-anak maupun dewasa. Memahami cara membuat dan melipat jaring-jaring ini membantu dalam memahami konsep geometri ruang tiga dimensi. Berikut langkah-langkah detailnya.
Material yang Dibutuhkan
Sebelum memulai, siapkan beberapa material sederhana. Keberhasilan pembuatan jaring-jaring kubus bergantung pada pemilihan material yang tepat dan sesuai dengan ukuran yang diinginkan. Perhatikan detailnya berikut ini:
- Kertas karton atau kertas manila: Material ini direkomendasikan karena cukup tebal dan mudah dilipat, menghasilkan kubus yang kokoh.
- Penggaris: Digunakan untuk mengukur dan membuat garis lurus yang presisi.
- Pensil: Untuk membuat sketsa jaring-jaring sebelum dipotong.
- Gunting atau cutter: Untuk memotong kertas dengan rapi.
- Lem atau selotip: (Opsional) Untuk merekatkan sisi-sisi jaring-jaring jika diperlukan, khususnya untuk kertas yang tipis.
Langkah-Langkah Pembuatan Jaring-Jaring Kubus Berukuran 10cm x 10cm
Berikut ini langkah-langkah pembuatan jaring-jaring kubus dengan ukuran sisi 10 cm. Anda dapat menyesuaikan ukuran ini sesuai kebutuhan. Perhatikan detail setiap langkah untuk hasil yang maksimal.
- Gambar sketsa: Pada kertas karton, gambarlah enam persegi dengan ukuran 10 cm x 10 cm yang tersusun membentuk salah satu pola jaring-jaring kubus. Ada beberapa pola jaring-jaring kubus yang mungkin, misalnya pola seperti huruf “T” atau pola yang terdiri dari empat persegi yang tersusun secara horizontal dengan dua persegi di atasnya. Pastikan jarak antar persegi terhubung dengan rapi.
- Potong: Setelah sketsa selesai, potonglah dengan hati-hati mengikuti garis yang telah dibuat. Gunakan gunting atau cutter sesuai kenyamanan Anda. Pastikan potongan rapi dan presisi untuk hasil lipatan yang baik.
- Lipat: Lipatlah setiap sisi persegi mengikuti garis yang telah dibuat. Pastikan lipatannya rapi dan tegas agar kubus yang terbentuk kokoh.
- Rekatkan (opsional): Jika menggunakan kertas yang tipis, rekatkan sisi-sisi yang berhimpitan menggunakan lem atau selotip. Hal ini akan membuat kubus lebih kuat dan tahan lama.
Ilustrasi Diagram Langkah Demi Langkah
Bayangkan sebuah diagram yang menampilkan enam persegi berukuran 10cm x 10cm disusun membentuk pola jaring-jaring kubus. Langkah pertama menunjukkan sketsa enam persegi tersebut. Langkah kedua menunjukkan enam persegi yang telah dipotong rapi. Langkah ketiga menampilkan enam persegi yang telah dilipat pada garis batasnya. Langkah terakhir menunjukkan kubus yang telah terbentuk sempurna, dengan keenam sisinya terhubung dengan rapi.
Setiap langkah diilustrasikan dengan gambar yang jelas dan mudah dipahami.
Cara Melipat Jaring-Jaring Menjadi Kubus, Bentuk jaring jaring kubus
Setelah jaring-jaring kubus dipotong, proses melipatnya menjadi kubus memerlukan ketelitian. Pastikan setiap lipatan presisi dan rapi. Awali dengan melipat salah satu sisi persegi yang berdekatan, kemudian lanjutkan dengan melipat sisi lainnya secara berurutan hingga membentuk struktur tiga dimensi kubus. Pastikan semua sisi terhubung dengan sempurna dan membentuk kubus yang utuh dan kokoh. Jika menggunakan lem atau selotip, pastikan perekat tersebut diaplikasikan dengan rapi dan merata agar tidak merusak bentuk kubus.
Penutupan: Bentuk Jaring Jaring Kubus
Memahami bentuk jaring-jaring kubus membuka jalan bagi pemahaman yang lebih dalam tentang geometri ruang dan aplikasinya. Kemampuan untuk mengenali, membedakan, dan bahkan menciptakan berbagai bentuk jaring-jaring kubus tidak hanya bermanfaat dalam konteks akademis, tetapi juga membuka peluang kreativitas dalam berbagai proyek praktis. Semoga uraian di atas memberikan wawasan yang berharga dan menginspirasi pembaca untuk lebih mengeksplorasi dunia geometri yang menarik ini.