Bentuk bidang, konsep dasar dalam geometri, menawarkan jendela menarik ke dunia bentuk dan ruang. Dari persegi sederhana hingga lengkungan kompleks, bentuk bidang berperan penting dalam berbagai aspek kehidupan kita, mulai dari arsitektur hingga teknologi canggih. Eksplorasi mengenai definisi, klasifikasi, perhitungan luas, dan penerapannya dalam berbagai bidang akan dibahas secara mendalam.
Pemahaman mendalam tentang bentuk bidang membuka jalan untuk memecahkan berbagai masalah praktis dan teoritis. Kita akan menjelajahi berbagai jenis bidang geometri, rumus perhitungan luasnya, dan aplikasinya dalam dunia nyata. Perjalanan kita akan mencakup bidang datar dan lengkung, dimensi dua dan tiga, bahkan menyinggung konsep bidang dalam dimensi yang lebih tinggi.
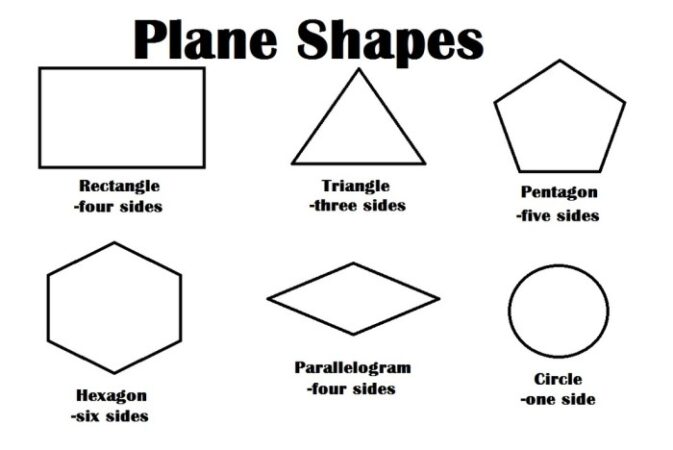
Definisi dan Klasifikasi Bidang Geometri: Bentuk Bidang
Bidang geometri merupakan konsep fundamental dalam matematika yang menggambarkan permukaan dua dimensi atau bagian dari ruang tiga dimensi. Pemahaman tentang bidang geometri sangat penting, baik dalam konteks matematika murni maupun aplikasinya dalam berbagai disiplin ilmu seperti arsitektur, teknik, dan desain. Klasifikasi bidang geometri didasarkan pada sifat-sifatnya, seperti kelengkungan dan keteraturan bentuk.
Jenis-jenis Bidang Geometri Dasar
Bidang geometri diklasifikasikan ke dalam beberapa jenis berdasarkan karakteristiknya. Pengelompokan ini membantu kita memahami dan menganalisis bentuk-bentuk geometri yang lebih kompleks.
- Bidang Datar: Bidang datar merupakan permukaan yang sepenuhnya rata dan tidak memiliki kelengkungan. Contohnya adalah permukaan meja, lantai, atau selembar kertas.
- Bidang Lengkung: Bidang lengkung memiliki kelengkungan, baik berupa permukaan cembung (melengkung keluar) maupun cekung (melengkung masuk). Contohnya adalah permukaan bola, permukaan bagian dalam mangkuk, atau permukaan lengkung pada bangunan modern.
- Bidang Beraturan: Bidang beraturan memiliki bentuk yang simetris dan teratur. Contohnya adalah bidang persegi, persegi panjang, lingkaran, atau segitiga sama sisi. Bidang-bidang ini seringkali digunakan sebagai dasar dalam konstruksi dan desain.
Contoh Bidang Geometri dalam Kehidupan Sehari-hari
Bidang geometri bukan hanya konsep abstrak, tetapi juga hadir di sekitar kita dalam berbagai bentuk.
- Bidang Datar: Permukaan dinding, lantai keramik, layar komputer, halaman buku.
- Bidang Lengkung: Permukaan bola basket, kubah masjid, permukaan bumi (secara pendekatan), lensa kacamata.
- Bidang Beraturan: Ubin lantai berbentuk persegi, jendela berbentuk persegi panjang, piring berbentuk lingkaran.
Perbandingan Karakteristik Beberapa Jenis Bidang Geometri
Tabel berikut membandingkan karakteristik beberapa jenis bidang geometri yang umum dijumpai.
| Jenis Bidang | Bentuk | Rumus Luas | Rumus Keliling |
|---|---|---|---|
| Persegi | Empat sisi sama panjang dan empat sudut siku-siku | s² (s = sisi) | 4s |
| Persegi Panjang | Dua pasang sisi sama panjang dan empat sudut siku-siku | p x l (p = panjang, l = lebar) | 2(p + l) |
| Lingkaran | Semua titik berjarak sama dari pusat | πr² (r = jari-jari) | 2πr |
| Segitiga Sama Sisi | Tiga sisi sama panjang dan tiga sudut sama besar (60°) | (√3/4)s² (s = sisi) | 3s |
| Segitiga Sembarang | Tiga sisi dengan panjang yang tidak harus sama | ½ x a x t (a = alas, t = tinggi) | a + b + c (a, b, c = panjang sisi) |
Perbedaan Bidang Datar dan Bidang Lengkung
Perbedaan mendasar antara bidang datar dan bidang lengkung terletak pada kelengkungannya. Bidang datar sepenuhnya rata, sehingga garis lurus yang ditarik di atasnya akan selalu berada pada bidang tersebut. Sebaliknya, bidang lengkung memiliki kelengkungan, sehingga garis lurus yang ditarik di atasnya akan meninggalkan bidang tersebut. Bayangkan sebuah bola (bidang lengkung): jika Anda menarik garis lurus di permukaannya, garis tersebut akan melengkung mengikuti permukaan bola, tidak akan tetap lurus seperti pada permukaan meja (bidang datar).
Perbedaan Bidang Dua Dimensi dan Tiga Dimensi
Bidang dua dimensi hanya memiliki panjang dan lebar, tidak memiliki ketebalan. Contohnya adalah gambar pada selembar kertas atau permukaan layar monitor. Bidang tiga dimensi memiliki panjang, lebar, dan tinggi. Contohnya adalah sebuah kubus, bola, atau ruangan.
Rumus dan Perhitungan Luas Bidang
Menghitung luas bidang merupakan konsep fundamental dalam geometri dan memiliki aplikasi luas dalam berbagai bidang, mulai dari arsitektur dan teknik sipil hingga desain grafis dan ilmu komputer. Memahami rumus dan metode perhitungan luas berbagai bentuk bidang merupakan kunci untuk menyelesaikan berbagai permasalahan yang berkaitan dengan ukuran dan ruang.
Rumus Luas Berbagai Bentuk Bidang
Berikut ini adalah ringkasan rumus perhitungan luas untuk beberapa bentuk bidang dasar. Penguasaan rumus-rumus ini akan memudahkan dalam menyelesaikan berbagai soal perhitungan luas.
- Persegi: Luas = sisi x sisi
- Persegi Panjang: Luas = panjang x lebar
- Segitiga: Luas = 1/2 x alas x tinggi
- Lingkaran: Luas = π x r² (dengan r adalah jari-jari)
- Jajargenjang: Luas = alas x tinggi
Contoh Perhitungan Luas Berbagai Bentuk Bidang
Mari kita lihat beberapa contoh soal dan penyelesaiannya untuk memperkuat pemahaman kita.
- Persegi dengan sisi 5 cm: Luas = 5 cm x 5 cm = 25 cm²
- Persegi Panjang dengan panjang 8 cm dan lebar 3 cm: Luas = 8 cm x 3 cm = 24 cm²
- Segitiga dengan alas 6 cm dan tinggi 4 cm: Luas = 1/2 x 6 cm x 4 cm = 12 cm²
- Lingkaran dengan jari-jari 7 cm: Luas = π x (7 cm)² ≈ 153.94 cm²
- Jajargenjang dengan alas 10 cm dan tinggi 6 cm: Luas = 10 cm x 6 cm = 60 cm²
Contoh Soal Cerita Luas Gabungan
Seringkali kita dihadapkan pada permasalahan yang melibatkan perhitungan luas gabungan beberapa bentuk bidang. Berikut contohnya:
Sebuah taman berbentuk persegi panjang dengan panjang 12 meter dan lebar 8 meter. Di tengah taman terdapat kolam renang berbentuk lingkaran dengan diameter 4 meter. Berapakah luas lahan taman yang tidak terpakai oleh kolam renang?
Penyelesaian: Luas taman = 12 m x 8 m = 96 m². Luas kolam = π x (2 m)² ≈ 12.57 m². Luas lahan tidak terpakai = 96 m²
-12.57 m² ≈ 83.43 m²
Perhitungan Luas Bidang Tidak Beraturan
Menghitung luas bidang tidak beraturan membutuhkan pendekatan yang berbeda. Salah satu metode yang dapat digunakan adalah metode integrasi numerik. Metode ini membagi bidang tidak beraturan menjadi sejumlah kecil bidang beraturan (misalnya persegi panjang atau trapesium), menghitung luas masing-masing bidang beraturan, dan menjumlahkannya untuk mendapatkan estimasi luas total. Tingkat akurasi metode ini bergantung pada seberapa kecil bidang-bidang beraturan yang digunakan.
Algoritma Perhitungan Luas Bidang Berdasarkan Koordinat Titik Sudut
Algoritma sederhana untuk menghitung luas bidang berdasarkan koordinat titik sudutnya dapat menggunakan metode “shoelace formula” atau “surveyor’s formula”. Metode ini melibatkan penjumlahan dan pengurangan koordinat titik-titik sudut secara berurutan. Rumus umumnya adalah:
Luas = 0.5
- | Σ (xᵢyᵢ₊₁
- xᵢ₊₁yᵢ) |
dimana i berurutan dari 1 hingga n (jumlah titik sudut), dan xₙ₊₁ = x₁, yₙ₊₁ = y₁. Perhitungan ini memberikan nilai absolut dari setengah jumlah perkalian silang koordinat-koordinat tersebut.
Penerapan Konsep Bidang dalam Kehidupan Nyata
Konsep bidang geometri, meskipun tampak sederhana, memiliki peran yang sangat krusial dalam berbagai aspek kehidupan kita. Pemahaman mendalam tentang bidang datar, bidang lengkung, dan sifat-sifatnya memungkinkan pengembangan teknologi dan desain yang inovatif serta efisien. Dari bangunan pencakar langit hingga karya seni yang memukau, bidang geometri selalu hadir sebagai elemen dasar yang membentuk dunia di sekitar kita.
Penerapan Bidang dalam Arsitektur dan Konstruksi
Dalam dunia arsitektur dan konstruksi, bidang merupakan elemen fundamental. Desain bangunan, baik yang sederhana maupun kompleks, bergantung pada perhitungan dan pemahaman yang akurat tentang bidang-bidang geometri. Contohnya, perencanaan struktur bangunan bertingkat tinggi melibatkan perhitungan yang cermat terkait beban dan tekanan yang bekerja pada berbagai bidang penyangga. Ketepatan dalam menentukan bidang-bidang ini sangat penting untuk memastikan stabilitas dan keamanan bangunan.
Penggunaan bidang juga terlihat jelas dalam desain fasad bangunan. Arsitek seringkali memanfaatkan berbagai bentuk dan susunan bidang untuk menciptakan estetika visual yang menarik dan fungsional. Contohnya, penggunaan bidang miring pada atap untuk mengoptimalkan penyaluran air hujan atau penggunaan bidang lengkung untuk menciptakan kesan dinamis dan modern pada desain bangunan.
Penerapan Bidang dalam Desain Grafis dan Seni Rupa
Bidang dalam desain grafis dan seni rupa berperan sebagai elemen dasar komposisi. Seniman dan desainer memanfaatkan bidang untuk menciptakan keseimbangan, kontras, dan fokus visual. Pemahaman tentang bagaimana bidang berinteraksi satu sama lain, baik dalam hal ukuran, bentuk, warna, dan tekstur, sangat penting untuk menghasilkan karya yang efektif dan menarik.
- Penggunaan bidang dalam logo perusahaan untuk menciptakan identitas visual yang unik dan mudah diingat.
- Penggunaan bidang dalam ilustrasi untuk membagi ruang dan menciptakan kedalaman.
- Penggunaan bidang dalam lukisan untuk menciptakan perspektif dan kesan ruang tiga dimensi.
Penerapan Bidang dalam Pembuatan Peta dan Sistem Navigasi
Peta dan sistem navigasi modern sangat bergantung pada representasi bidang datar sebagai model permukaan bumi. Meskipun bumi berbentuk bulat, untuk keperluan praktis, peta seringkali menggunakan proyeksi bidang untuk menampilkan informasi geografis. Sistem navigasi GPS juga menggunakan koordinat bidang untuk menentukan lokasi dan menghitung jarak.
Akurasi dalam penggambaran bidang pada peta sangat penting untuk menghindari kesalahan dalam navigasi. Pemahaman tentang distorsi yang terjadi akibat proyeksi bidang pada peta juga krusial untuk interpretasi yang tepat.
Peran Bidang dalam Pengembangan Teknologi
Konsep bidang berperan penting dalam berbagai aspek pengembangan teknologi, khususnya dalam desain produk dan manufaktur. Proses pembuatan berbagai produk, dari komponen elektronik hingga suku cadang otomotif, melibatkan perhitungan dan manipulasi bidang geometri yang presisi. Penggunaan software CAD (Computer-Aided Design) memungkinkan desainer untuk memodelkan dan memanipulasi bidang-bidang tiga dimensi dengan tingkat akurasi yang tinggi.
Contohnya, dalam desain mobil, bidang-bidang aerodinamis yang tepat sangat penting untuk meminimalkan hambatan udara dan meningkatkan efisiensi bahan bakar. Dalam industri manufaktur, pemahaman tentang bidang-bidang yang terlibat dalam proses pemotongan, pembubutan, dan pengelasan sangat penting untuk menghasilkan produk dengan kualitas yang tinggi.
Pemahaman tentang bidang geometri, termasuk sifat-sifatnya seperti luas permukaan, volume, dan hubungan antar bidang, sangat penting dalam menyelesaikan permasalahan teknik dan rekayasa. Kemampuan untuk menganalisis dan memanipulasi bidang geometri secara akurat merupakan kunci keberhasilan dalam berbagai proyek konstruksi, desain produk, dan pengembangan teknologi. Ketidaktepatan dalam pemahaman ini dapat berakibat fatal, baik secara finansial maupun keselamatan.
Bidang dalam Dimensi yang Lebih Tinggi
Konsep bidang, yang familiar dalam geometri dua dimensi sebagai garis lurus dan dalam geometri tiga dimensi sebagai bidang datar, dapat diperluas ke dimensi yang lebih tinggi. Pemahaman tentang bidang dalam dimensi yang lebih tinggi penting dalam berbagai bidang, termasuk matematika tingkat lanjut, fisika, dan ilmu komputer, khususnya dalam konteks ruang vektor dan aljabar linear.
Bidang dalam Ruang Tiga Dimensi
Dalam ruang tiga dimensi, bidang didefinisikan sebagai himpunan semua titik yang memenuhi persamaan linear tertentu. Persamaan umum bidang dalam ruang tiga dimensi dapat ditulis sebagai Ax + By + Cz + D = 0, di mana A, B, dan C adalah konstanta yang tidak semuanya nol, dan D adalah konstanta. Contohnya, bidang x + 2y – 3z + 4 = 0 mewakili sebuah bidang di ruang tiga dimensi.
Setiap titik (x, y, z) yang memenuhi persamaan ini terletak pada bidang tersebut. Contoh konkretnya adalah bidang yang melalui titik-titik (0, 0, 4/3), (0, 2, 0), dan (4, 0, 0). Ini membentuk sebuah bidang yang membagi ruang tiga dimensi menjadi dua bagian.
Perbedaan Bidang Dua dan Tiga Dimensi
Perbedaan utama antara bidang dalam ruang dua dan tiga dimensi terletak pada jumlah variabel dan representasinya. Dalam ruang dua dimensi, bidang (atau garis) didefinisikan oleh persamaan linear dengan dua variabel (misalnya, y = mx + c), sedangkan dalam ruang tiga dimensi, bidang didefinisikan oleh persamaan linear dengan tiga variabel (Ax + By + Cz + D = 0). Dalam ruang dua dimensi, bidang hanya dapat membagi ruang menjadi dua bagian, sementara dalam ruang tiga dimensi, bidang membagi ruang menjadi dua bagian semi-ruang.
Perbandingan Persamaan Umum Bidang, Bentuk bidang
| Dimensi | Persamaan Umum | Penjelasan |
|---|---|---|
| Dua Dimensi | Ax + By + C = 0 | Representasi garis lurus. A, B, dan C adalah konstanta. |
| Tiga Dimensi | Ax + By + Cz + D = 0 | Representasi bidang datar. A, B, C, dan D adalah konstanta. |
Konsep Bidang Hiper (Hyperplane)
Konsep bidang dapat diperluas ke dimensi yang lebih tinggi. Dalam ruang empat dimensi atau lebih tinggi, analog dari bidang disebut hiperbidang (hyperplane). Bayangkan sebuah ruang empat dimensi. Hiperbidang dalam ruang ini dapat divisualisasikan sebagai “bidang” yang membagi ruang empat dimensi menjadi dua bagian. Meskipun sulit untuk dibayangkan secara visual, kita dapat mendefinisikannya secara matematis.
Misalnya, dalam ruang empat dimensi dengan koordinat (x, y, z, w), sebuah hiperbidang dapat didefinisikan oleh persamaan Ax + By + Cz + Dw + E = 0, di mana A, B, C, D, dan E adalah konstanta. Analogi yang dapat kita gunakan adalah bayangan sebuah bidang tiga dimensi yang diproyeksikan ke ruang dua dimensi – kita kehilangan satu dimensi, tetapi kita masih dapat menggambarkan esensinya.
Hiperbidang dalam dimensi yang lebih tinggi memiliki sifat-sifat serupa dengan bidang dalam ruang tiga dimensi, seperti membagi ruang menjadi dua setengah ruang dan memiliki persamaan linear yang mendefinisikannya.
Ekstensi Konsep Bidang ke Dimensi yang Lebih Tinggi
Konsep bidang dalam dimensi yang lebih tinggi memiliki aplikasi luas dalam matematika dan fisika. Dalam matematika, hiperbidang digunakan dalam aljabar linear, geometri analitik, dan topologi. Dalam fisika, konsep ini relevan dalam mekanika kuantum dan teori relativitas, di mana ruang-waktu sering dimodelkan sebagai ruang dengan empat atau lebih dimensi. Pemahaman tentang hiperbidang penting untuk menganalisis dan memodelkan fenomena-fenomena kompleks dalam dimensi yang lebih tinggi, yang melampaui kemampuan visualisasi manusia, tetapi tetap dapat dipahami dan dimanipulasi melalui alat-alat matematis.
Ringkasan Akhir
Perjalanan kita mengeksplorasi dunia bentuk bidang telah membawa kita melewati berbagai konsep dan aplikasi yang menarik. Dari rumus luas sederhana hingga penerapannya dalam teknologi modern, bentuk bidang menunjukkan keindahan dan kekuatan matematika dalam menjelaskan dunia di sekitar kita. Memahami bentuk bidang bukan hanya untuk keperluan akademis, tetapi juga kunci untuk inovasi dan pemecahan masalah di berbagai disiplin ilmu.