Bentuk bentuk bangun ruang – Bentuk-bentuk bangun ruang merupakan topik menarik dalam matematika yang mempelajari berbagai macam objek tiga dimensi. Dari kubus sederhana yang kita temui setiap hari hingga bentuk-bentuk kompleks seperti kerucut dan bola, bangun ruang hadir dalam berbagai variasi dan memiliki sifat-sifat unik. Pemahaman mendalam tentang bangun ruang tidak hanya penting dalam matematika, tetapi juga berperan krusial dalam berbagai bidang seperti arsitektur, teknik, dan desain.
Kita akan menjelajahi berbagai jenis bangun ruang, mulai dari definisi dasar hingga rumus perhitungan volume dan luas permukaannya. Selain itu, kita akan mengkaji sifat-sifat unik masing-masing bangun ruang dan melihat penerapannya dalam kehidupan sehari-hari. Dengan pemahaman yang komprehensif, kita dapat mengapresiasi keindahan dan kompleksitas bentuk-bentuk geometris tiga dimensi ini.
Pengenalan Bangun Ruang: Bentuk Bentuk Bangun Ruang
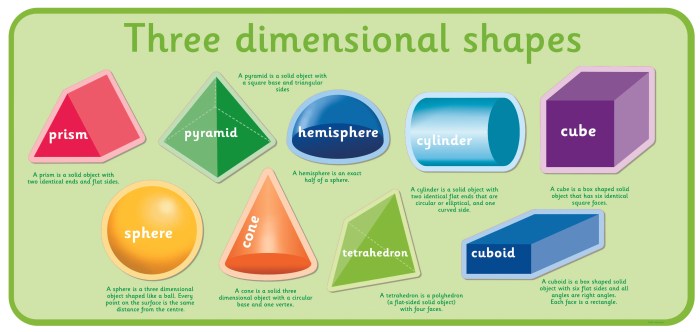
Bangun ruang merupakan objek tiga dimensi yang memiliki volume dan dibatasi oleh permukaan-permukaan. Studi tentang bangun ruang merupakan bagian penting dalam geometri, membantu kita memahami dan menganalisis bentuk-bentuk objek di dunia nyata. Pemahaman tentang bangun ruang juga penting dalam berbagai bidang, mulai dari arsitektur hingga teknik.
Contoh bangun ruang sederhana antara lain kubus, balok, dan bola. Bentuk-bentuk ini mudah dikenali dan sering dijumpai dalam kehidupan sehari-hari.
Jenis-jenis Bangun Ruang dan Ciri-cirinya, Bentuk bentuk bangun ruang
Berikut tabel yang merangkum beberapa jenis bangun ruang beserta ciri-ciri utamanya:
| Nama Bangun Ruang | Ciri-ciri Utama | Jumlah Sisi | Jumlah Rusuk |
|---|---|---|---|
| Kubus | Keenam sisinya berbentuk persegi dan kongruen. Semua rusuknya sama panjang. | 6 | 12 |
| Balok | Terdiri dari enam sisi berbentuk persegi panjang. Sisi-sisi yang berhadapan kongruen. | 6 | 12 |
| Prisma Segitiga | Dua sisi berbentuk segitiga yang kongruen dan sejajar, serta tiga sisi berbentuk persegi panjang. | 5 | 9 |
| Limas Segi Empat | Satu sisi berbentuk segi empat dan empat sisi berbentuk segitiga yang bertemu pada satu titik puncak. | 5 | 8 |
| Bola | Permukaannya lengkung dan setiap titik pada permukaannya berjarak sama terhadap titik pusat. | 1 | 0 |
Perbedaan Bangun Ruang Sisi Datar dan Bangun Ruang Sisi Lengkung
Bangun ruang sisi datar memiliki sisi-sisi yang berupa bidang datar, seperti kubus, balok, dan prisma. Sedangkan bangun ruang sisi lengkung memiliki setidaknya satu sisi yang berupa permukaan lengkung, contohnya bola, tabung, dan kerucut. Perbedaan mendasar terletak pada bentuk sisi penyusun bangun ruang tersebut.
Bangun Ruang dalam Kehidupan Sehari-hari
Banyak bangun ruang yang kita temui dalam kehidupan sehari-hari. Pemahaman tentang bentuk dan sifatnya membantu kita dalam berbagai aktivitas.
- Kubus: Kotak kemasan makanan, dadu, rubik. Kubus memiliki sifat-sifat yang membuatnya ideal sebagai kemasan karena efisiensi ruang dan kekuatan strukturnya.
- Balok: Buku, lemari, bata. Bentuk balok memungkinkan penataan yang efisien dalam penyimpanan dan konstruksi.
- Bola: Bola sepak, bola basket, planet bumi. Bentuk bola memiliki luas permukaan minimum untuk volume tertentu, membuatnya ideal untuk objek yang bergerak seperti bola.
Rumus dan Perhitungan Bangun Ruang

Memahami rumus dan perhitungan bangun ruang sangat penting dalam berbagai bidang, mulai dari arsitektur dan teknik sipil hingga desain produk dan matematika. Kemampuan menghitung volume dan luas permukaan bangun ruang memungkinkan kita untuk menyelesaikan masalah praktis dan merancang objek tiga dimensi dengan tepat. Berikut ini penjelasan mengenai rumus dan contoh perhitungan untuk beberapa bangun ruang dasar.
Rumus Volume Kubus, Balok, dan Prisma Segitiga
Ketiga bangun ruang ini memiliki rumus volume yang relatif sederhana. Kubus, dengan enam sisi yang sama panjang, memiliki volume yang mudah dihitung. Balok, dengan tiga pasang sisi yang berhadapan dan sejajar, juga memiliki perhitungan volume yang straightforward. Prisma segitiga, yang merupakan gabungan dari dua segitiga kongruen sebagai alas dan tiga persegi panjang sebagai sisi tegak, memiliki perhitungan volume yang sedikit lebih kompleks, namun tetap mudah dipahami.
- Kubus: Volume = s 3 (s = panjang rusuk)
- Balok: Volume = p x l x t (p = panjang, l = lebar, t = tinggi)
- Prisma Segitiga: Volume = ½ x a x t x tinggi prisma (a = alas segitiga, t = tinggi segitiga)
Contoh Perhitungan Volume Kubus
Misalnya, kita ingin menghitung volume kubus dengan panjang rusuk 10 cm. Dengan menggunakan rumus Volume = s 3, kita masukkan nilai s = 10 cm:
Volume = 10 cm x 10 cm x 10 cm = 1000 cm3
Jadi, volume kubus tersebut adalah 1000 cm 3.
Perhitungan Luas Permukaan Balok
Luas permukaan balok merupakan jumlah luas keenam sisinya. Untuk menghitungnya, kita perlu mengetahui panjang, lebar, dan tinggi balok. Rumusnya dapat dijabarkan sebagai berikut:
Luas Permukaan = 2 x (p x l + p x t + l x t) (p = panjang, l = lebar, t = tinggi)
Sebagai contoh, untuk balok dengan panjang 12 cm, lebar 8 cm, dan tinggi 5 cm:
Luas Permukaan = 2 x (12 cm x 8 cm + 12 cm x 5 cm + 8 cm x 5 cm) = 2 x (96 cm2 + 60 cm 2 + 40 cm 2) = 2 x 196 cm 2 = 392 cm 2
Luas permukaan balok tersebut adalah 392 cm 2.
Rumus Luas Permukaan dan Volume Tabung, Kerucut, dan Bola
Bangun ruang seperti tabung, kerucut, dan bola memiliki rumus yang sedikit lebih kompleks dibandingkan kubus dan balok. Rumus-rumus ini melibatkan penggunaan π (pi), yang nilainya sekitar 3.14.
- Tabung: Volume = πr 2t (r = jari-jari, t = tinggi); Luas Permukaan = 2πr 2 + 2πrt
- Kerucut: Volume = (1/3)πr 2t (r = jari-jari, t = tinggi); Luas Permukaan = πr 2 + πr√(r 2 + t 2)
- Bola: Volume = (4/3)πr 3 (r = jari-jari); Luas Permukaan = 4πr 2
Contoh Perhitungan Volume Kerucut
Mari hitung volume kerucut dengan jari-jari 7 cm dan tinggi 15 cm. Kita gunakan rumus Volume = (1/3)πr 2t:
Volume = (1/3) x 3.14 x (7 cm)2 x 15 cm = (1/3) x 3.14 x 49 cm 2 x 15 cm ≈ 769.3 cm 3
Volume kerucut tersebut kira-kira 769.3 cm 3.
Sifat-Sifat Bangun Ruang
Memahami sifat-sifat bangun ruang merupakan kunci untuk menguasai geometri tiga dimensi. Sifat-sifat ini meliputi jumlah sisi, rusuk, dan titik sudut, serta karakteristik unik lainnya yang membedakan satu bangun ruang dengan bangun ruang lainnya. Pemahaman ini penting dalam berbagai aplikasi, mulai dari arsitektur hingga desain industri.
Sifat-Sifat Kubus
Kubus, sebagai bangun ruang sisi datar yang paling sederhana, memiliki sifat-sifat yang khas. Setiap sisinya berbentuk persegi dan kongruen (sama bentuk dan ukuran). Jumlah sisi kubus adalah 6, jumlah rusuknya 12, dan jumlah titik sudutnya 8. Semua sudutnya merupakan sudut siku-siku (90 derajat).
Perbedaan Sifat Kubus dan Balok
Meskipun sekilas mirip, kubus dan balok memiliki perbedaan mendasar dalam sifat-sifatnya. Balok juga memiliki 6 sisi, 12 rusuk, dan 8 titik sudut, namun sisi-sisi balok tidak semuanya berbentuk persegi, melainkan persegi panjang. Hanya sisi-sisi yang berhadapan saja yang kongruen. Sudut-sudutnya juga merupakan sudut siku-siku.
Perbandingan Sifat Prisma Segitiga dan Limas Segitiga
Prisma segitiga dan limas segitiga merupakan contoh bangun ruang yang menunjukkan perbedaan signifikan dalam sifat-sifatnya.
- Prisma segitiga memiliki dua sisi alas yang kongruen berbentuk segitiga dan tiga sisi tegak berbentuk persegi panjang. Jumlah rusuknya 9 dan jumlah titik sudutnya 6.
- Limas segitiga memiliki satu sisi alas berbentuk segitiga dan tiga sisi tegak berbentuk segitiga. Jumlah rusuknya 6 dan jumlah titik sudutnya 4.
Sifat-Sifat Bola
Bola merupakan bangun ruang sisi lengkung yang unik. Sifat utamanya ditentukan oleh jari-jari (r) dan diameter (d) nya. Diameter bola adalah jarak terpanjang yang dapat diukur di dalam bola, dan sama dengan dua kali jari-jari (d = 2r). Setiap titik pada permukaan bola berjarak sama terhadap titik pusat bola.
Perbandingan Bangun Ruang Sisi Datar dan Bangun Ruang Sisi Lengkung
Bangun ruang sisi datar dan bangun ruang sisi lengkung memiliki perbedaan mendasar dalam bentuk dan sifat-sifatnya.
| Sifat | Bangun Ruang Sisi Datar (Contoh: Kubus, Balok) | Bangun Ruang Sisi Lengkung (Contoh: Bola, Tabung) |
|---|---|---|
| Bentuk Sisi | Datar (persegi, persegi panjang, segitiga, dll.) | Lengkung (lingkaran, permukaan lengkung) |
| Jumlah Sisi | Berhingga | Satu sisi lengkung |
| Rusuk | Berupa garis lurus | Tidak memiliki rusuk |
Penerapan Bangun Ruang dalam Kehidupan Sehari-hari
Bangun ruang, seperti kubus, balok, prisma, limas, tabung, kerucut, dan bola, bukan sekadar konsep geometri abstrak. Keberadaannya sangat vital dan terintegrasi dalam berbagai aspek kehidupan kita, mulai dari konstruksi bangunan hingga kemasan produk dan dunia seni.
Penerapan Bangun Ruang dalam Konstruksi Bangunan
Bangun ruang berperan krusial dalam perencanaan dan pembangunan berbagai jenis bangunan. Penggunaan bentuk-bentuk geometri ini memastikan struktur yang kokoh, efisien, dan estetis.
- Kubus dan balok sering ditemukan pada desain bangunan modern, menciptakan kesan minimalis dan fungsional.
- Prisma segitiga dan limas digunakan pada konstruksi atap bangunan, khususnya untuk bangunan dengan desain yang unik dan menawan.
- Tabung dan silinder sering diterapkan pada desain menara, tangki air, atau elemen arsitektur lainnya.
- Bola dapat diaplikasikan pada desain kubah bangunan, menciptakan ruang yang luas dan megah.
- Kerucut terkadang digunakan sebagai elemen dekoratif atau fungsional pada atap bangunan tertentu.
Penggunaan Bangun Ruang dalam Kemasan Produk
Bentuk bangun ruang juga sangat berpengaruh pada desain kemasan produk. Pemilihan bentuk yang tepat tidak hanya mempertimbangkan estetika, tetapi juga faktor fungsionalitas, efisiensi penyimpanan, dan perlindungan produk.
- Kubus dan balok banyak digunakan untuk kemasan produk makanan, minuman, dan barang-barang lainnya karena kemudahan penyimpanan dan efisiensi ruang.
- Tabung digunakan untuk kemasan produk seperti pasta gigi, minuman kaleng, dan beberapa jenis makanan.
- Kerucut sering ditemukan pada kemasan es krim atau beberapa jenis makanan ringan.
Penerapan Bangun Ruang dalam Dunia Seni dan Desain
Dalam dunia seni dan desain, bangun ruang menjadi elemen dasar dalam menciptakan karya-karya yang estetis dan bermakna. Seniman dan desainer memanfaatkan berbagai bentuk bangun ruang untuk mengekspresikan ide dan gagasan mereka.
Patung-patung, instalasi seni, dan desain produk seringkali menggabungkan berbagai bangun ruang untuk menciptakan karya yang dinamis dan menarik. Contohnya, penggunaan kubus dan balok dalam karya seni minimalis, atau kombinasi berbagai bangun ruang dalam desain furnitur modern.
Ilustrasi Penggunaan Kubus dalam Arsitektur Modern
Bayangkan sebuah bangunan perkantoran modern dengan fasad yang didominasi oleh susunan kubus-kubus besar yang saling berkaitan. Kubus-kubus tersebut memiliki ukuran dan warna yang bervariasi, menciptakan efek visual yang dinamis dan menarik. Beberapa kubus berfungsi sebagai balkon, sementara yang lain membentuk ruang-ruang kantor yang luas dan terang. Kesederhanaan bentuk kubus diimbangi oleh penggunaan material modern seperti kaca dan baja, menghasilkan tampilan yang elegan dan futuristik.
Penerapan kubus dalam desain ini tidak hanya menciptakan estetika yang modern, tetapi juga memberikan fleksibilitas dalam pengaturan ruang dalam.
Penggunaan Bangun Ruang dalam Bidang Teknologi
Penggunaan bangun ruang dalam teknologi sangat luas, mulai dari desain perangkat keras hingga simulasi dan pemodelan 3D. Bentuk-bentuk geometri ini menjadi dasar dalam perancangan dan pengembangan berbagai teknologi.
Contohnya, dalam desain chip komputer, bentuk-bentuk bangun ruang yang presisi sangat penting untuk optimasi kinerja dan efisiensi. Selain itu, dalam teknologi pemodelan 3D, bangun ruang digunakan untuk menciptakan model virtual objek dan lingkungan, yang berguna dalam berbagai bidang seperti arsitektur, teknik, dan animasi.
Hubungan Antar Bangun Ruang
Berbagai bangun ruang, meskipun tampak berbeda, seringkali memiliki hubungan erat satu sama lain. Memahami hubungan ini membantu kita untuk lebih mudah memahami sifat-sifat dan karakteristik masing-masing bangun ruang, serta memudahkan dalam menyelesaikan permasalahan geometri yang lebih kompleks. Berikut ini akan dibahas beberapa hubungan antar bangun ruang yang penting.
Hubungan Kubus dan Balok
Kubus dan balok merupakan dua bangun ruang yang sangat dekat hubungannya. Balok dapat dianggap sebagai generalisasi dari kubus. Kubus merupakan kasus khusus dari balok, di mana semua sisinya memiliki panjang yang sama. Dengan kata lain, setiap sisi kubus merupakan persegi, sedangkan sisi balok dapat berupa persegi panjang. Baik kubus maupun balok memiliki enam sisi, dua belas rusuk, dan delapan titik sudut.
Kemiripan dan Perbedaan Prisma dan Limas
Prisma dan limas merupakan dua bangun ruang yang memiliki beberapa kesamaan dan perbedaan yang signifikan. Perbedaan utama terletak pada bentuk alas dan atapnya. Prisma memiliki dua alas yang kongruen dan sejajar, serta sisi-sisi tegak yang berbentuk persegi panjang. Sementara itu, limas hanya memiliki satu alas dan beberapa sisi tegak yang bertemu pada satu titik puncak. Baik prisma maupun limas dapat memiliki alas berupa segitiga, segi empat, atau segi banyak lainnya.
Kemiripannya terletak pada keduanya memiliki sisi-sisi tegak yang menghubungkan alas dan atap (atau puncak).
Hubungan Tabung, Kerucut, dan Bola
Ketiga bangun ruang ini dapat dihubungkan melalui konsep rotasi. Bayangkan sebuah persegi panjang diputar mengelilingi salah satu sisinya; maka akan terbentuk sebuah tabung. Jika sebuah segitiga siku-siku diputar mengelilingi salah satu kakinya, akan terbentuk sebuah kerucut. Sedangkan, jika sebuah setengah lingkaran diputar mengelilingi diameternya, akan terbentuk sebuah bola. Ketiganya memiliki kesamaan dalam bentuk simetri putar, meskipun bentuk dan sifat-sifatnya berbeda.
Diagram hubungan ini dapat dibayangkan sebagai berikut: Tabung memiliki alas dan atap yang berupa lingkaran, kerucut memiliki satu alas lingkaran dan satu titik puncak, sedangkan bola merupakan bangun ruang yang seluruh titik permukaannya berjarak sama terhadap pusatnya. Ketiga bangun ruang ini dapat divisualisasikan sebagai hasil rotasi bangun datar.
Bangun Ruang Gabungan
Banyak bangun ruang yang kita temui dalam kehidupan sehari-hari merupakan gabungan dari beberapa bangun ruang sederhana. Penggabungan ini dapat dilakukan dengan berbagai cara, seperti menyatukan, menumpuk, atau menggabungkan bagian-bagian dari bangun ruang yang berbeda.
Contoh Bangun Ruang Gabungan Kubus dan Balok
Contoh sederhana bangun ruang gabungan kubus dan balok adalah sebuah rumah minimalis. Rumah tersebut dapat disederhanakan sebagai gabungan beberapa kubus (untuk bagian utama rumah) dan balok (untuk bagian tambahan seperti garasi atau teras). Bentuk-bentuk lain yang lebih kompleks juga dapat dibentuk dari gabungan kubus dan balok, tergantung pada kreativitas dan desain yang diinginkan. Misalnya, sebuah bangunan bertingkat dapat divisualisasikan sebagai tumpukan kubus dan balok dengan ukuran dan posisi yang berbeda.
Penutup

Memahami bentuk-bentuk bangun ruang membuka pintu menuju pemahaman yang lebih dalam tentang dunia geometri tiga dimensi. Dari kubus sederhana hingga bentuk-bentuk yang lebih kompleks, setiap bangun ruang memiliki karakteristik unik dan peran penting dalam berbagai aspek kehidupan. Semoga uraian ini telah memberikan gambaran yang komprehensif dan menginspirasi eksplorasi lebih lanjut tentang dunia menarik bangun ruang.