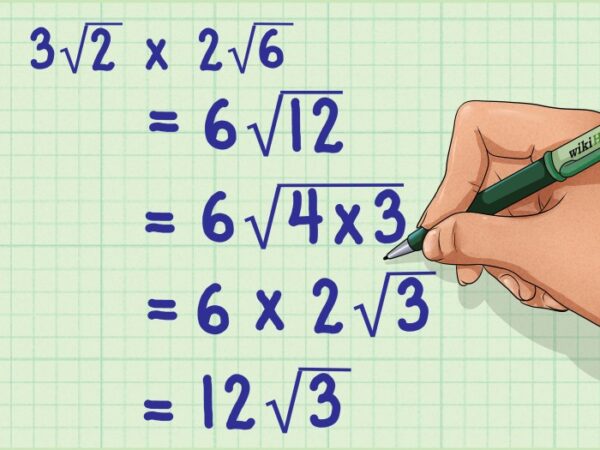Akar 6 adalah, dalam dunia matematika, sebuah bilangan irasional yang menarik. Ia tidak dapat dinyatakan sebagai pecahan sederhana, dan representasi desimalnya berlanjut tanpa batas tanpa pola berulang. Namun, pemahaman tentang akar 6 sangat penting, karena ia muncul dalam berbagai aplikasi praktis, mulai dari perhitungan geometri hingga masalah fisika dan teknik.
Nilai numerik akar 6 kira-kira 2,449489743. Kita dapat mendekati nilai ini melalui berbagai metode, seperti metode iteratif Newton-Raphson. Lebih jauh lagi, akar 6 memiliki hubungan erat dengan konsep bilangan irasional dan berperan penting dalam berbagai persamaan dan rumus matematika. Memahami sifat dan aplikasinya akan membuka wawasan yang lebih dalam tentang dunia matematika dan aplikasinya di kehidupan nyata.
Nilai Akar 6

Akar kuadrat dari 6, dinotasikan sebagai √6, merupakan bilangan irasional yang nilainya terletak di antara 2 dan 3. Ini berarti tidak dapat dinyatakan sebagai pecahan sederhana dan memiliki angka desimal yang tidak berulang dan tidak berakhir. Pemahaman mendalam tentang nilai dan perhitungan akar 6 penting dalam berbagai bidang matematika dan ilmu terapan.
Nilai Numerik Akar 6
Nilai numerik akar kuadrat dari 6 secara tepat tidak dapat dinyatakan, karena merupakan bilangan irasional. Namun, kita dapat mendekati nilainya hingga tingkat presisi tertentu. Representasi desimal akar 6 hingga 10 tempat desimal adalah 2.4494897428.
Perhitungan Akar 6 dengan Metode Iteratif (Newton-Raphson)
Metode Newton-Raphson merupakan salah satu metode numerik yang efektif untuk menghitung akar kuadrat. Metode ini bekerja dengan iterasi, mendekati akar secara bertahap. Rumus iterasi untuk mencari akar kuadrat dari suatu bilangan x adalah:
xn+1 = 0.5
(xn + x/x n)
Dimana x n adalah perkiraan ke-n dan x adalah bilangan yang akar kuadratnya ingin dicari (dalam kasus ini, 6). Dengan memulai dari tebakan awal (misalnya, x 0 = 2), kita dapat melakukan iterasi berulang kali hingga mencapai tingkat presisi yang diinginkan. Semakin banyak iterasi, semakin akurat hasilnya.
Perbandingan Akar 6 dengan Akar Kuadrat Bilangan Terdekat
Tabel berikut membandingkan akar 6 dengan akar kuadrat dari bilangan bulat terdekat, yaitu 5 dan 7. Perbedaan dan persentase perbedaan dihitung relatif terhadap akar 6.
| Bilangan | Akar Kuadrat | Perbedaan dengan Akar 6 | Persentase Perbedaan |
|---|---|---|---|
| 5 | 2.2360679775 | 0.2134217653 | 8.71% |
| 6 | 2.4494897428 | 0 | 0% |
| 7 | 2.6457513111 | 0.1962615683 | 7.99% |
Posisi Akar 6 pada Garis Bilangan Real
Pada garis bilangan real, akar 6 terletak di antara bilangan bulat 2 dan 3, lebih dekat ke 2. Secara visual, kita dapat membayangkannya sebagai titik yang berada kira-kira 2/3 jarak antara 2 dan 3. Karena √6 ≈ 2.449, titik tersebut akan berada lebih dekat ke 2 daripada ke 3.
Akar 6 dalam Konteks Matematika
Akar 6, dinotasikan sebagai √6, merupakan bilangan irasional yang sering dijumpai dalam berbagai perhitungan matematika. Memahami sifat dan karakteristiknya penting untuk menguasai operasi matematika yang lebih kompleks.
Penyederhanaan Akar 6
Akar 6 tidak dapat disederhanakan lebih lanjut menjadi bentuk akar yang lebih sederhana karena 6 hanya memiliki faktor prima 2 dan 3. Tidak ada faktor kuadrat sempurna yang dapat dikeluarkan dari akar tersebut. Bentuk paling sederhana dari √6 tetaplah √6.
Contoh Penggunaan Akar 6 dalam Persamaan Matematika
Akar 6 sering muncul dalam persamaan yang melibatkan teorema Pythagoras atau dalam penyelesaian persamaan kuadrat. Sebagai contoh, perhatikan persamaan x² = 6. Penyelesaiannya adalah x = ±√6.
Akar 6 sebagai Bilangan Irasional, Akar 6 adalah
Bilangan irasional adalah bilangan yang tidak dapat dinyatakan sebagai pecahan dari dua bilangan bulat. Akar 6 termasuk bilangan irasional karena nilai desimalnya tidak berulang dan tidak berakhir (≈ 2.4494897…). Ini berbeda dengan bilangan rasional seperti 1/2 atau 3/4 yang memiliki representasi desimal berulang atau berakhir.
Operasi Matematika pada Akar 6
Operasi matematika dasar seperti penjumlahan, pengurangan, perkalian, dan pembagian dapat dilakukan pada akar 6, namun hasilnya seringkali masih berupa bilangan irasional. Perlu diingat aturan perkalian dan pembagian akar:
- √a
– √b = √(a*b) - √a / √b = √(a/b)
Contohnya, √6 + 2√6 = 3√6. Sedangkan √6 x √2 = √12 = 2√3.
Contoh Soal dan Penyelesaian
Berikut contoh soal yang melibatkan akar 6 dan penyelesaiannya:
Soal: Tentukan panjang sisi miring segitiga siku-siku dengan panjang sisi siku-sikunya 2 dan √24.
Penyelesaian:
- Gunakan teorema Pythagoras: c² = a² + b², dimana c adalah panjang sisi miring, dan a dan b adalah panjang sisi siku-siku.
- Substitusikan nilai yang diketahui: c² = 2² + (√24)² = 4 + 24 = 28
- Akar kuadratkan kedua ruas: c = √28 = √(4 x 7) = 2√7
- Jadi, panjang sisi miring segitiga tersebut adalah 2√7.
Akar 6 dalam Aplikasi Praktis
Meskipun tidak sering muncul seperti akar kuadrat dari angka sederhana, akar 6 memiliki peran penting dalam berbagai aplikasi praktis, khususnya di bidang geometri, fisika, dan beberapa cabang ilmu lainnya. Keberadaannya seringkali tersembunyi dalam rumus dan perhitungan yang lebih kompleks, namun pemahaman akan akar 6 sangat membantu dalam menyelesaikan masalah-masalah tersebut.
Aplikasi Akar 6 dalam Geometri
Akar 6 sering muncul dalam perhitungan geometri yang melibatkan bangun ruang dan bidang. Salah satu contohnya adalah menghitung panjang diagonal suatu persegi panjang. Jika kita memiliki persegi panjang dengan panjang sisi a dan b, maka panjang diagonalnya (d) dapat dihitung menggunakan teorema Pythagoras: d = √(a² + b²). Jika a dan b memiliki nilai yang menghasilkan a² + b² = 6, maka panjang diagonalnya adalah √6.
Sebagai contoh konkret, bayangkan sebuah persegi panjang dengan panjang sisi 1 dan √5. Panjang diagonalnya akan menjadi √(1² + (√5)²) = √(1 + 5) = √6.
Akar 6 dalam Perhitungan Fisika dan Teknik
Dalam fisika dan teknik, akar 6 dapat muncul dalam berbagai konteks, seringkali sebagai bagian dari persamaan yang lebih besar. Misalnya, dalam perhitungan terkait vektor atau dalam mekanika, khususnya dalam menentukan resultan beberapa gaya yang bekerja pada suatu titik. Akar 6 mungkin menjadi bagian dari penyelesaian persamaan yang kompleks.
Sebagai ilustrasi, bayangkan skenario di mana tiga gaya dengan besar yang sama bekerja pada suatu titik dengan sudut tertentu yang menghasilkan resultan gaya dengan besar yang melibatkan akar 6 dalam perhitungannya. Tentu saja, ini hanya salah satu contoh ilustrasi, dan persamaan yang sebenarnya akan jauh lebih kompleks bergantung pada skenario fisika yang spesifik.
Penggunaan Akar 6 dalam Statistik dan Pemrograman
Meskipun kurang umum dibandingkan di bidang geometri dan fisika, akar 6 juga dapat muncul dalam beberapa aplikasi statistik dan pemrograman. Misalnya, dalam perhitungan deviasi standar atau dalam algoritma tertentu yang melibatkan optimasi atau simulasi, akar 6 mungkin muncul sebagai bagian dari perhitungan numerik yang lebih kompleks.
Contohnya, dalam simulasi distribusi probabilitas tertentu, nilai akar 6 bisa menjadi faktor skala atau konstanta dalam rumus yang digunakan. Namun, ini memerlukan konteks yang lebih spesifik dalam algoritma pemrograman atau model statistik tertentu.
Contoh Skenario Dunia Nyata
Bayangkan seorang arsitek merancang sebuah gedung dengan denah persegi panjang yang memiliki luas 6 meter persegi dan rasio aspek tertentu. Untuk menentukan panjang diagonal gedung tersebut, arsitek tersebut akan menggunakan perhitungan yang melibatkan akar 6, mengingat luas persegi panjang dan teorema Pythagoras.
Tiga Aplikasi Praktis Akar 6
- Perhitungan Panjang Diagonal: Akar 6 muncul saat menghitung panjang diagonal persegi panjang dengan panjang sisi tertentu yang memenuhi persamaan Pythagoras, seperti yang telah dijelaskan sebelumnya.
- Analisis Vektor dalam Fisika: Dalam perhitungan resultan beberapa vektor gaya, akar 6 dapat menjadi bagian dari solusi persamaan vektor yang lebih kompleks, tergantung pada besar dan arah vektor-vektor tersebut.
- Optimasi Algoritma dalam Pemrograman: Dalam algoritma tertentu, khususnya yang berhubungan dengan optimasi atau simulasi, akar 6 dapat menjadi konstanta atau faktor skala dalam perhitungan numerik.
Representasi Akar 6
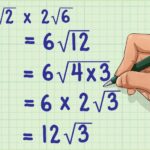
Akar 6, dilambangkan sebagai √6, merupakan bilangan irasional, artinya tidak dapat dinyatakan sebagai pecahan sederhana dari dua bilangan bulat. Meskipun demikian, akar 6 dapat direpresentasikan dalam berbagai bentuk, memungkinkan kita untuk memahaminya dan mengaplikasikannya dalam berbagai konteks matematika dan komputasi.
Representasi Akar 6 sebagai Pecahan
Akar 6 tidak dapat dinyatakan sebagai pecahan sederhana. Sifatnya sebagai bilangan irasional berarti representasi pecahannya akan selalu berupa pendekatan, di mana angka di belakang koma akan terus berlanjut tanpa pola berulang. Semakin banyak digit yang digunakan, semakin akurat pendekatan tersebut.
Representasi Akar 6 dalam Notasi Ilmiah
Dalam notasi ilmiah, akar 6 dapat ditulis sebagai 2,449 × 10 0. Notasi ini berguna untuk merepresentasikan bilangan yang sangat besar atau sangat kecil dengan cara yang ringkas dan mudah dibaca. Angka 2,449 merupakan nilai pendekatan akar 6, dan 10 0 menunjukkan bahwa angka tersebut berada dalam orde satuan.
Representasi Visual Akar 6
Akar 6 dapat direpresentasikan secara visual sebagai panjang sebuah segmen garis. Bayangkan sebuah segitiga siku-siku dengan dua sisi siku-sikunya masing-masing memiliki panjang 1 dan √5. Hipotenusa segitiga tersebut, sesuai dengan teorema Pythagoras (a² + b² = c²), akan memiliki panjang √(1² + (√5)²) = √6. Panjang hipotenusa ini secara visual merepresentasikan nilai akar 6.
Pentingnya Memahami Representasi Berbeda Akar 6
Memahami berbagai representasi akar 6, baik sebagai pendekatan desimal, notasi ilmiah, maupun representasi geometrik, sangat penting karena memungkinkan kita untuk bekerja dengan bilangan irasional ini dalam berbagai konteks. Kemampuan untuk beralih antar representasi memperluas pemahaman kita tentang konsep matematika dan memudahkan penerapannya dalam pemecahan masalah.
Representasi Akar 6 dalam Program Komputer
Dalam bahasa pemrograman Python, akar 6 dapat diwakilkan menggunakan fungsi math.sqrt() dari modul math. Berikut contohnya:
import math
akar_enam = math.sqrt(6)
print(akar_enam) # Output: 2.449489742783178
Kode di atas akan menampilkan nilai pendekatan akar 6. Nilai ini merupakan representasi numerik akar 6 yang akurat hingga batas presisi yang ditentukan oleh kemampuan pemrosesan komputer.
Penutup: Akar 6 Adalah
Kesimpulannya, akar 6, meskipun tampak sederhana, menyimpan kekayaan matematis yang signifikan. Ketidakmampuannya untuk disederhanakan menjadi pecahan biasa justru menunjukkan keindahan matematika yang tersembunyi. Pemahaman mendalam tentang akar 6 dan representasinya membuka jalan untuk menyelesaikan berbagai permasalahan dalam berbagai disiplin ilmu, menekankan pentingnya eksplorasi lebih lanjut dalam dunia bilangan irasional.