
Akar 32 adalah sebuah konsep matematika yang mungkin tampak sederhana, namun menyimpan kekayaan pemahaman yang menarik. Memahami akar 32 tidak hanya melibatkan perhitungan numerik, tetapi juga membuka pintu untuk eksplorasi geometri dan aplikasi dalam berbagai persamaan matematika. Dari penyederhanaan akar 32 hingga penerapannya dalam menghitung panjang sisi suatu bangun geometri, bahasan ini akan mengungkap keindahan tersembunyi di balik angka sederhana ini.
Mencari nilai akar 32 melibatkan proses faktorisasi prima untuk menyederhanakannya ke bentuk paling sederhana, yaitu 4√2. Nilai desimalnya dapat dihitung dengan menggunakan kalkulator atau metode numerik, dan kemudian dapat diaplikasikan dalam berbagai konteks, termasuk perhitungan luas dan panjang sisi bangun geometri seperti persegi, persegi panjang, dan segitiga siku-siku. Lebih lanjut, akar 32 juga dapat diintegrasikan ke dalam berbagai operasi matematika dasar, seperti penjumlahan, pengurangan, perkalian, dan pembagian.
Penguraian Bilangan 32: Akar 32 Adalah

Menentukan akar kuadrat dari 32, √32, memerlukan pemahaman tentang faktorisasi prima dan penyederhanaan bentuk akar. Proses ini melibatkan penguraian bilangan 32 menjadi faktor-faktor primanya, lalu mengidentifikasi faktor-faktor yang merupakan kuadrat sempurna untuk menyederhanakan ekspresi akar.
Faktorisasi Prima Bilangan 32
Faktorisasi prima dari 32 adalah proses memecah bilangan 32 menjadi perkalian bilangan prima saja. Bilangan prima adalah bilangan bulat lebih besar dari 1 yang hanya habis dibagi 1 dan dirinya sendiri. Langkah-langkah faktorisasi prima 32 adalah sebagai berikut:
- 32 dibagi 2 menghasilkan 16.
- 16 dibagi 2 menghasilkan 8.
- 8 dibagi 2 menghasilkan 4.
- 4 dibagi 2 menghasilkan 2.
- 2 adalah bilangan prima.
Oleh karena itu, faktorisasi prima dari 32 adalah 2 x 2 x 2 x 2 x 2 = 2 5.
Penyederhanaan Akar Pangkat Dua dari 32
Setelah mendapatkan faktorisasi prima, kita dapat menyederhanakan √32. Kita mencari pasangan bilangan yang sama dalam faktorisasi prima untuk mengeluarkannya dari dalam tanda akar.
Karena 32 = 2 5 = 2 4 x 2, maka √32 dapat ditulis sebagai √(2 4 x 2). Karena 2 4 adalah kuadrat sempurna (2 4 = 16), maka kita dapat menyederhanakannya:
√(24 x 2) = √2 4 x √2 = 2 2√2 = 4√2
Identifikasi Faktor Kuadrat Sempurna dari 32
Faktor kuadrat sempurna dari 32 adalah bilangan yang merupakan hasil kali bilangan bulat dengan dirinya sendiri. Dalam faktorisasi prima 32 (2 5), 2 4 (atau 16) adalah faktor kuadrat sempurna terbesar.
Langkah-Langkah Penyederhanaan √32
Tabel berikut merangkum langkah-langkah penyederhanaan √32:
| Langkah | Operasi | Hasil | Penjelasan |
|---|---|---|---|
| 1 | Faktorisasi prima 32 | 25 | Menguraikan 32 menjadi perkalian bilangan prima. |
| 2 | Mengidentifikasi faktor kuadrat sempurna | 24 x 2 | Mencari faktor yang merupakan kuadrat sempurna (24 = 16). |
| 3 | Menyederhanakan akar kuadrat | √(24 x 2) | Memisahkan faktor kuadrat sempurna dari faktor lainnya di dalam akar. |
| 4 | Mengeluarkan faktor kuadrat sempurna dari akar | √24 x √2 | Akar kuadrat dari 24 adalah 22. |
| 5 | Hasil akhir | 4√2 | Bentuk paling sederhana dari √32. |
Nilai Akar 32 dalam Bentuk Desimal
Akar kuadrat dari 32 (√32) bukanlah bilangan bulat, sehingga nilainya berupa bilangan desimal yang irasional. Menentukan nilai desimalnya memerlukan perhitungan, baik menggunakan kalkulator maupun metode numerik. Berikut ini akan diuraikan perhitungan nilai desimal √32 hingga tiga tempat desimal, beserta perbandingannya dengan akar pangkat dua bilangan bulat terdekat, menggunakan dua metode berbeda.
Perhitungan Nilai Desimal √32 Menggunakan Kalkulator
Metode paling sederhana untuk menentukan nilai desimal √32 adalah dengan menggunakan kalkulator. Cukup masukkan angka 32 dan tekan tombol akar kuadrat (√). Hasil yang ditampilkan akan berupa nilai desimal √32. Kalkulator ilmiah umumnya akan menampilkan nilai dengan tingkat presisi yang tinggi. Untuk keperluan kita, kita akan membulatkan hasil hingga tiga tempat desimal.
Dengan menggunakan kalkulator, kita dapatkan nilai √32 ≈ 5.657. Angka ini merupakan pendekatan karena nilai sebenarnya dari √32 memiliki angka desimal yang tak berujung.
Perhitungan Nilai Desimal √32 Menggunakan Metode Numerik (Metode Iterasi Newton-Raphson)
Metode numerik, seperti metode iterasi Newton-Raphson, dapat digunakan untuk menghitung akar kuadrat secara iteratif. Metode ini dimulai dengan sebuah tebakan awal, lalu secara berulang memperbaiki tebakan tersebut hingga mencapai tingkat akurasi yang diinginkan. Meskipun rumus dan perhitungannya lebih kompleks, metode ini memberikan pemahaman yang lebih mendalam tentang bagaimana nilai desimal √32 diperoleh.
Meskipun detail perhitungan metode Newton-Raphson cukup rumit untuk dijelaskan secara rinci di sini, prinsip dasarnya adalah dengan menggunakan rumus iteratif untuk memperbaharui tebakan nilai akar secara berulang. Dengan cukup banyak iterasi, kita akan mendekati nilai √32 yang akurat. Sebagai contoh, jika kita mulai dengan tebakan awal 5, iterasi berulang akan menghasilkan nilai yang semakin mendekati 5.657.
Perbandingan dengan Akar Bilangan Bulat Terdekat
Bilangan bulat terdekat yang akar kuadratnya mendekati √32 adalah 5 (√25 = 5) dan 6 (√36 = 6). Nilai √32 (≈ 5.657) terletak di antara kedua nilai tersebut, lebih dekat ke 6 daripada ke 5.
Ketelitian Nilai Desimal √32
Nilai desimal √32 yang dihitung, baik menggunakan kalkulator maupun metode numerik, merupakan pendekatan. Nilai sebenarnya dari √32 adalah bilangan irasional, yang berarti memiliki angka desimal yang tak berujung dan tak berpola. Ketelitian hasil perhitungan bergantung pada jumlah desimal yang ditampilkan atau tingkat akurasi yang ditentukan dalam metode numerik. Pembulatan hingga tiga tempat desimal memberikan nilai yang cukup akurat untuk kebanyakan keperluan praktis.
Akar 32 dalam Konteks Geometri
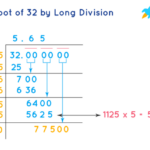
Akar kuadrat dari 32, atau √32, sering muncul dalam perhitungan geometri yang melibatkan luas dan panjang sisi bangun datar. Nilai √32 sendiri dapat disederhanakan menjadi 4√2, yang memudahkan dalam beberapa perhitungan. Berikut beberapa contoh penerapan √32 dalam konteks geometri.
Luas Persegi dan Panjang Sisi
Sebuah persegi dengan luas 32 satuan luas memiliki panjang sisi yang sama dengan √32 satuan panjang. Hal ini karena rumus luas persegi adalah sisi x sisi, sehingga untuk mendapatkan panjang sisi, kita perlu menghitung akar kuadrat dari luasnya. Oleh karena itu, panjang sisi persegi tersebut adalah 4√2 satuan panjang, atau sekitar 5.66 satuan panjang.
Luas Persegi Panjang dan Hubungan Panjang Lebar
Persegi panjang dengan luas 32 satuan luas dapat memiliki berbagai kombinasi panjang dan lebar. Misalnya, panjangnya 8 satuan dan lebarnya 4 satuan (8 x 4 = 32). Namun, kita juga bisa memiliki persegi panjang dengan panjang 4√2 satuan dan lebar 2√2 satuan (4√2 x 2√2 = 32). Dalam kasus ini, panjang dan lebarnya berhubungan dengan √32 karena perkaliannya menghasilkan luas 32.
Panjang Diagonal Persegi dan Persegi Panjang
Teorema Pythagoras sangat berguna untuk menghitung panjang diagonal. Pada persegi dengan sisi √32, diagonalnya dapat dihitung dengan rumus d = √(sisi² + sisi²) = √(32 + 32) = √64 = 8 satuan panjang. Untuk persegi panjang dengan panjang 8 dan lebar 4, diagonalnya adalah √(8² + 4²) = √(64 + 16) = √80 = 4√5 satuan panjang. Meskipun tidak secara langsung menggunakan √32, perhitungan ini menunjukkan bagaimana akar kuadrat digunakan dalam konteks diagonal bangun datar.
Segitiga Siku-Siku dengan Sisi √32
Bayangkan sebuah segitiga siku-siku dengan salah satu sisi tegak lurusnya berukuran √32 satuan panjang. Jika sisi lainnya diketahui, misalnya 4 satuan panjang, maka sisi miring (hipotenusa) dapat dihitung menggunakan Teorema Pythagoras: hipotenusa = √((√32)² + 4²) = √(32 + 16) = √48 = 4√3 satuan panjang. Dengan demikian, √32 berperan sebagai salah satu unsur dalam perhitungan panjang sisi segitiga siku-siku.
Penerapan √32 dalam Perhitungan Geometri Sederhana
Akar 32, atau bentuk sederhananya 4√2, muncul dalam berbagai perhitungan geometri dasar, terutama yang melibatkan luas dan panjang sisi bangun datar. Kemampuan untuk menyederhanakan bentuk akar dan menggunakan Teorema Pythagoras menjadi kunci dalam menyelesaikan masalah-masalah geometri yang melibatkan √32.
Akar 32 dan Operasi Matematika Lainnya
Akar kuadrat dari 32, atau √32, merupakan bilangan irasional yang sering muncul dalam berbagai perhitungan matematika. Memahami bagaimana √32 berinteraksi dengan operasi matematika dasar sangat penting untuk menyelesaikan berbagai macam permasalahan matematika, baik yang sederhana maupun yang kompleks.
Penggunaan √32 dalam Operasi Matematika Dasar, Akar 32 adalah
Bilangan √32 dapat digunakan dalam penjumlahan, pengurangan, perkalian, dan pembagian seperti bilangan lainnya. Perlu diingat bahwa √32 merupakan nilai pendekatan, sehingga hasil perhitungan juga akan berupa nilai pendekatan. Berikut beberapa contohnya:
- Penjumlahan: 5 + √32 ≈ 5 + 5,66 = 10,66
- Pengurangan: 10 – √32 ≈ 10 – 5,66 = 4,34
- Perkalian: 3 × √32 ≈ 3 × 5,66 = 16,98
- Pembagian: 20 / √32 ≈ 20 / 5,66 ≈ 3,53
Penyederhanaan √32 dengan Akar Pangkat Dua Lainnya
√32 dapat disederhanakan dengan memanfaatkan sifat perkalian akar. Karena 32 = 16 × 2, maka √32 = √(16 × 2) = √16 × √2 = 4√2. Dengan bentuk sederhana ini, perhitungan menjadi lebih mudah, terutama jika melibatkan akar pangkat dua lainnya.
- Contoh: √32 × √8 = 4√2 × 2√2 = 8 × 2 = 16
- Contoh: √32 / √2 = 4√2 / √2 = 4
Penggunaan √32 dalam Persamaan Matematika Sederhana
Akar 32 seringkali muncul dalam persamaan kuadrat dan persamaan lainnya. Kemampuan untuk memanipulasi dan menyederhanakan √32 sangat krusial dalam menyelesaikan persamaan-persamaan tersebut.
- Contoh: x² = 32. Maka, x = ±√32 = ±4√2
Contoh Soal dan Penyelesaian
Berikut contoh soal yang melibatkan √32 dan penyelesaiannya:
Soal: Tentukan nilai dari (√32 + 2√2)²
Penyelesaian:
- Sederhanakan √32 menjadi 4√2.
- Substitusikan ke dalam persamaan: (4√2 + 2√2)²
- Gabungkan suku-suku sejenis: (6√2)²
- Kuadratkan: 36 × 2 = 72
Jadi, nilai dari (√32 + 2√2)² adalah 72.
Penutup
Kesimpulannya, akar 32, meskipun tampak sederhana, menawarkan pemahaman yang kaya dan luas dalam matematika. Dari proses penyederhanaan hingga aplikasinya dalam geometri dan operasi matematika lainnya, angka ini menunjukkan bagaimana konsep matematika dasar dapat memiliki implikasi yang mendalam dan luas. Dengan memahami akar 32, kita dapat memperluas pemahaman kita tentang konsep akar kuadrat dan aplikasinya dalam berbagai bidang.






