Akar 1 sama dengan 1, pernyataan sederhana yang menyimpan kedalaman matematis yang menarik. Pernyataan ini, meskipun tampak sepele, menjadi fondasi bagi pemahaman konsep akar dan operasinya dalam berbagai cabang matematika, mulai dari aritmatika dasar hingga kalkulus tingkat lanjut. Lebih dari sekadar jawaban sederhana, “akar 1 sama dengan 1” membuka pintu bagi eksplorasi konsep matematika yang lebih kompleks dan aplikasinya dalam dunia nyata.
Dalam uraian berikut, kita akan menelusuri berbagai interpretasi “akar 1 sama dengan 1”, mulai dari pemahamannya dalam matematika dasar hingga penerapannya dalam persamaan matematika yang lebih rumit. Kita akan melihat bagaimana konsep ini divisualisasikan dan dibandingkan dengan akar dari angka lain, mengungkapkan keindahan dan kesederhanaan yang tersembunyi di balik pernyataan matematis yang fundamental ini.
Arti dan Interpretasi “Akar 1 Sama Dengan”
Frasa “akar 1 sama dengan” mungkin tampak sederhana, namun menyimpan beragam interpretasi matematis tergantung konteks penggunaannya. Pemahaman yang tepat sangat penting untuk menghindari kesalahpahaman, terutama dalam perhitungan dan penyelesaian masalah matematika.
Interpretasi Matematis “Akar 1 Sama Dengan”
Secara umum, “akar 1 sama dengan” merujuk pada operasi akar pangkat n dari 1. Akar pangkat n dari suatu bilangan x didefinisikan sebagai bilangan y yang jika dipangkatkan n akan menghasilkan x (y n = x). Dalam kasus akar 1, nilai y yang memenuhi persamaan tersebut akan selalu 1, terlepas dari nilai n (asalkan n bilangan bulat positif).
Konteks Penggunaan dan Makna
Frasa ini sering muncul dalam berbagai konteks matematika, mulai dari aljabar dasar hingga kalkulus. Dalam aljabar dasar, frasa ini mungkin digunakan untuk menyelesaikan persamaan sederhana. Dalam kalkulus, dapat muncul dalam konteks limit atau turunan. Maknanya selalu konsisten, yaitu menunjukkan hasil operasi akar pangkat n dari 1 yang bernilai 1.
Perbedaan Akar Kuadrat dan Akar Pangkat Lainnya
Meskipun akar 1 selalu bernilai 1 untuk semua akar pangkat n, terdapat perbedaan dalam notasi dan interpretasi. Akar kuadrat (akar pangkat 2) dinotasikan dengan simbol √, sementara akar pangkat lainnya (akar pangkat 3, 4, dan seterusnya) dinotasikan dengan n√. Namun, hasil operasi akar pangkat berapa pun dari 1 tetap sama, yaitu 1.
Perbandingan Akar Kuadrat 1 dengan Akar Pangkat Lain dari 1
Tabel berikut membandingkan hasil operasi akar pangkat berbeda dari 1. Perhatikan bahwa meskipun notasi berbeda, hasilnya selalu konsisten.
| Akar Pangkat | Notasi | Operasi | Hasil |
|---|---|---|---|
| Kuadrat | √1 | √1 | 1 |
| Kubik | 3√1 | 3√1 | 1 |
| Pangkat Empat | 4√1 | 4√1 | 1 |
| Pangkat n | n√1 | n√1 | 1 |
Contoh Kalimat “Akar 1 Sama Dengan”
Berikut beberapa contoh kalimat yang menggunakan frasa “akar 1 sama dengan” dalam konteks yang berbeda:
- Dalam penyelesaian persamaan kuadrat, kita menemukan bahwa akar 1 sama dengan 1.
- Sebagai ilustrasi sederhana, akar pangkat tiga dari 1 sama dengan 1.
- Rumus tersebut menunjukkan bahwa, terlepas dari nilai n, akar pangkat n dari 1 sama dengan 1.
Penggunaan dalam Matematika Dasar: Akar 1 Sama Dengan

Konsep akar kuadrat 1, yang hasilnya selalu 1, merupakan fondasi penting dalam pemahaman matematika dasar. Pengenalan konsep ini biasanya dimulai dengan pemahaman perkalian dan kebalikannya, yaitu akar kuadrat. Memahami akar 1 sama dengan 1 membantu siswa dalam membangun landasan yang kuat untuk operasi matematika yang lebih kompleks di masa mendatang.
Penjelasan Konsep Akar Kuadrat 1
Dalam matematika dasar, akar kuadrat suatu bilangan didefinisikan sebagai bilangan yang jika dikuadratkan (dikalikan dengan dirinya sendiri) akan menghasilkan bilangan tersebut. Dengan demikian, akar kuadrat dari 1 adalah 1 karena 1 x 1 = 1. Konsep ini dijelaskan dengan sederhana dan visual, seringkali menggunakan contoh-contoh konkret seperti luas persegi.
Contoh Soal Matematika Dasar yang Melibatkan Akar Kuadrat 1
Berikut adalah contoh soal yang melibatkan akar kuadrat 1, yang seringkali diintegrasikan dengan operasi matematika lainnya:
- Hitunglah nilai dari √1 + 2 x 3.
- Sederhanakan ekspresi berikut: (√1)2 + 5 – 2.
- Jika luas sebuah persegi adalah 1 cm 2, berapakah panjang sisi persegi tersebut?
Langkah-Langkah Penyelesaian Soal Matematika Dasar yang Melibatkan Akar 1
Penyelesaian soal yang melibatkan akar 1 umumnya mengikuti urutan operasi matematika standar (prioritas operasi). Pertama, selesaikan operasi dalam tanda kurung, lalu perkalian dan pembagian, kemudian penjumlahan dan pengurangan. Akar kuadrat 1 selalu disederhanakan menjadi 1 sebelum operasi lain dilakukan.
- Identifikasi operasi matematika yang terlibat.
- Sederhanakan akar kuadrat 1 menjadi 1.
- Ikuti urutan operasi matematika standar untuk menyelesaikan soal.
Contoh Soal Cerita yang Melibatkan Konsep Akar 1
Sebuah kotak mainan berbentuk persegi memiliki luas 1 meter persegi. Berapakah panjang sisi kotak mainan tersebut?
Penyelesaian: Luas persegi = sisi x sisi. Karena luasnya 1 meter persegi, maka sisi x sisi = 1. Oleh karena itu, panjang sisi kotak mainan adalah √1 = 1 meter.
Penggunaan Akar 1 dalam Operasi Matematika Sederhana
Akar 1 (yang sama dengan 1) dapat digunakan dalam berbagai operasi matematika sederhana:
| Operasi | Contoh | Hasil |
|---|---|---|
| Penjumlahan | 1 + 1 | 2 |
| Pengurangan | 5 – 1 | 4 |
| Perkalian | 3 x 1 | 3 |
| Pembagian | 10 / 1 | 10 |
Aplikasi dalam Matematika Lanjutan
Konsep sederhana “akar 1 sama dengan 1” terlihat trivial, namun berperan fundamental dalam berbagai cabang matematika tingkat lanjut. Kehadirannya yang tampak sepele ini menjadi dasar untuk pemahaman konsep yang lebih kompleks dan aplikasinya sangat luas, dari aljabar hingga persamaan diferensial.
Aplikasi dalam Aljabar
Dalam aljabar, akar 1 sama dengan 1 merupakan identitas perkalian. Konsep ini mendasari berbagai teorema dan operasi aljabar. Sebagai contoh, penggunaan sifat ini sangat penting dalam penyederhanaan ekspresi aljabar dan penyelesaian persamaan. Identitas ini memungkinkan kita untuk memanipulasi persamaan tanpa mengubah nilai aslinya, menjadikannya alat yang krusial dalam berbagai pembuktian matematis.
Penerapan dalam Kalkulus
Konsep akar 1 sama dengan 1 memiliki implikasi penting dalam kalkulus, terutama dalam limit dan turunan. Ketika kita mencari limit suatu fungsi, nilai 1 seringkali muncul sebagai hasil limit tersebut. Begitu pula, dalam menghitung turunan suatu fungsi, nilai konstanta 1 akan mempengaruhi hasil turunan tersebut, meskipun secara langsung tidak menunjukkan perubahan yang signifikan.
Penggunaan identitas ini membantu dalam menyederhanakan perhitungan dan memperjelas langkah-langkah dalam proses diferensiasi dan integrasi.
Peran dalam Geometri Analitik
Dalam geometri analitik, konsep akar 1 sama dengan 1 terlihat dalam persamaan garis dan kurva. Misalnya, persamaan garis y = x dapat dilihat sebagai representasi dari konsep ini, di mana nilai x dan y selalu sama. Lebih lanjut, konsep ini berperan dalam transformasi geometri, di mana operasi skalanya dengan faktor 1 tidak mengubah bentuk atau ukuran objek geometri.
Peran Penting Akar 1 dalam Persamaan Matematika Tingkat Lanjut
Akar 1 sama dengan 1, sebuah pernyataan sederhana, namun merupakan landasan bagi berbagai teorema dan konsep penting dalam matematika tingkat lanjut. Identitas ini memungkinkan manipulasi aljabar yang tepat dan memudahkan penyelesaian persamaan kompleks. Kehadirannya yang konsisten menunjukkan peran fundamental dalam keseluruhan struktur matematika.
Contoh Penerapan dalam Persamaan Diferensial
Pertimbangkan persamaan diferensial sederhana: dy/dx = 1. Solusi dari persamaan ini adalah y = x + C, di mana C adalah konstanta integrasi. Dalam persamaan ini, konstanta 1 menentukan kemiringan garis solusi. Meskipun terlihat sederhana, persamaan ini merupakan contoh bagaimana konsep akar 1 sama dengan 1 berperan dalam menentukan bentuk solusi persamaan diferensial.
Persamaan diferensial yang lebih kompleks juga bergantung pada konsep dasar ini, meskipun kemunculannya mungkin tidak selalu sejelas dalam contoh ini.
Representasi Visual “Akar 1 Sama Dengan 1”
Memahami konsep akar kuadrat, khususnya akar kuadrat dari 1, dapat dibantu dengan representasi visual. Representasi ini memungkinkan pemahaman yang lebih intuitif, terutama bagi pemula. Berikut beberapa cara untuk memvisualisasikan akar kuadrat 1.
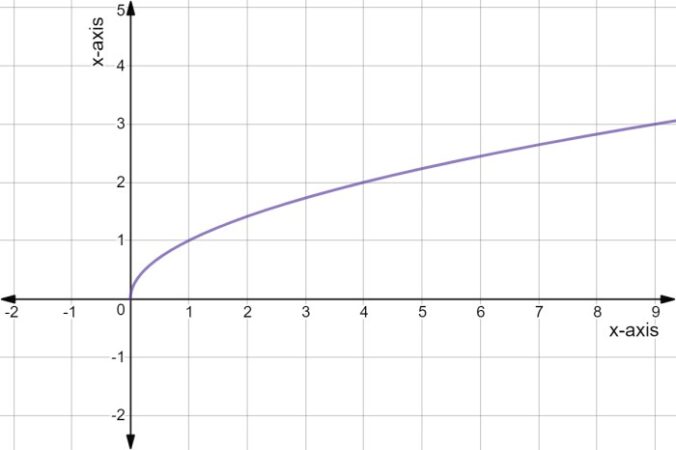
Representasi pada Bidang Koordinat Kartesius
Pada bidang koordinat kartesius, akar kuadrat 1 direpresentasikan sebagai titik (1,0). Ini karena akar kuadrat 1 adalah 1, dan titik ini terletak pada sumbu x dengan jarak 1 satuan dari titik asal (0,0). Tidak ada representasi lain yang signifikan pada bidang koordinat kartesius untuk akar kuadrat 1 karena nilainya hanya satu. Nilai ini mewakili jarak dari titik asal ke titik (1,0) pada sumbu x positif.
Representasi pada Garis Bilangan
Pada garis bilangan, akar kuadrat 1 ditunjukkan sebagai titik yang terletak tepat pada angka 1. Angka 1 dan akar kuadrat 1 berhimpit pada garis bilangan karena √1 = 1. Ini menunjukkan secara sederhana bahwa akar kuadrat dari 1 adalah 1 itu sendiri. Garis bilangan memberikan representasi satu dimensi yang mudah dipahami.
Representasi Geometri dengan Persegi
Konsep akar kuadrat dapat dihubungkan dengan geometri, khususnya luas persegi. Sebuah persegi dengan sisi sepanjang 1 satuan memiliki luas 1 satuan persegi. Akar kuadrat dari luas persegi (1 satuan persegi) sama dengan panjang sisi persegi tersebut (1 satuan). Ini memberikan representasi visual yang konkrit tentang hubungan antara akar kuadrat dan luas bangun geometri.
Representasi Visual untuk Siswa SD
Untuk siswa SD, penjelasan dapat difokuskan pada analogi sederhana. Misalnya, kita bisa menggunakan gambar persegi dengan sisi 1 cm. Kita dapat menjelaskan bahwa luas persegi tersebut adalah 1 cm², dan akar kuadrat dari 1 cm² adalah panjang sisi persegi, yaitu 1 cm. Atau, kita dapat menggunakan contoh benda-benda konkret yang berjumlah satu, lalu mengaitkannya dengan konsep akar kuadrat 1.
Penggunaan gambar dan contoh konkret akan mempermudah pemahaman mereka.
Perbandingan dengan Konsep Akar Lain

Akar kuadrat dari 1, atau √1, merupakan konsep dasar dalam matematika yang seringkali dianggap sederhana. Namun, memahami perbandingannya dengan akar kuadrat angka lain membantu kita mengapresiasi sifat uniknya dan implikasinya dalam berbagai perhitungan matematika. Perbandingan ini akan mengungkap perbedaan dan persamaan dalam perhitungan dan penerapannya, serta dampaknya terhadap hasil akhir.
Konsep akar kuadrat secara umum merujuk pada bilangan yang, jika dikuadratkan (dikalikan dengan dirinya sendiri), menghasilkan angka di dalam tanda akar. √1 = 1 karena 1 x 1 = 1. Namun, bagaimana √1 berbeda dengan akar kuadrat angka lain, seperti √4 atau √9?
Perbedaan Sifat Akar Kuadrat 1 dengan Angka Lain
| Sifat | √1 | √4 | √9 |
|---|---|---|---|
| Nilai | 1 | 2 | 3 |
| Keunikan | Satu-satunya akar kuadrat yang sama dengan dirinya sendiri. | Bilangan bulat positif. | Bilangan bulat positif. |
| Penerapan dalam persamaan | Menyederhanakan persamaan. | Memperkenalkan solusi tambahan dalam persamaan kuadrat. | Memperkenalkan solusi tambahan dalam persamaan kuadrat. |
| Representasi Geometris | Sisi persegi dengan luas 1 satuan. | Sisi persegi dengan luas 4 satuan. | Sisi persegi dengan luas 9 satuan. |
Perbedaan dalam Perhitungan dan Penerapan
Perbedaan utama terletak pada nilai dan konsekuensinya dalam perhitungan. √1 selalu menghasilkan 1, sedangkan akar kuadrat angka lain menghasilkan nilai yang berbeda. Ini berdampak signifikan pada penyederhanaan persamaan aljabar dan geometri. Misalnya, dalam persamaan x² = 1, solusi hanya x = 1 dan x = -1. Namun, dalam persamaan x² = 4, solusi menjadi x = 2 dan x = -2.
Perbedaan ini muncul karena √1 hanya memiliki satu akar positif, sementara akar kuadrat angka lain memiliki dua akar (positif dan negatif).
Implikasi dalam Berbagai Konteks Matematika
Perbedaan ini memiliki implikasi luas dalam berbagai bidang matematika. Dalam kalkulus, turunan dari √x di titik x=1 akan berbeda dengan turunannya di titik x=4 atau x=9. Dalam geometri, √1 mewakili panjang sisi persegi dengan luas 1, sedangkan √4 dan √9 mewakili sisi persegi dengan luas 4 dan 9. Perbedaan ini juga terlihat dalam trigonometri dan berbagai aplikasi matematika lainnya.
Sebagai contoh, dalam persamaan fisika yang melibatkan perhitungan jarak, kecepatan, atau percepatan, penggunaan √1 akan menghasilkan hasil yang berbeda dibandingkan dengan penggunaan akar kuadrat angka lain. Hal ini karena akar kuadrat seringkali mewakili besaran fisik seperti kecepatan atau jarak yang nilainya bergantung pada kuadrat besaran lainnya.
Ulasan Penutup
Kesimpulannya, “akar 1 sama dengan 1” bukanlah sekadar rumus matematis sederhana, melainkan sebuah konsep dasar yang memiliki peran penting dalam berbagai bidang matematika. Pemahaman yang mendalam tentang konsep ini membuka jalan bagi pemahaman konsep-konsep matematika yang lebih kompleks dan aplikasinya dalam berbagai disiplin ilmu. Dari pemahaman dasar hingga penerapan tingkat lanjut, konsep ini terus relevan dan menjadi landasan penting dalam perkembangan matematika.