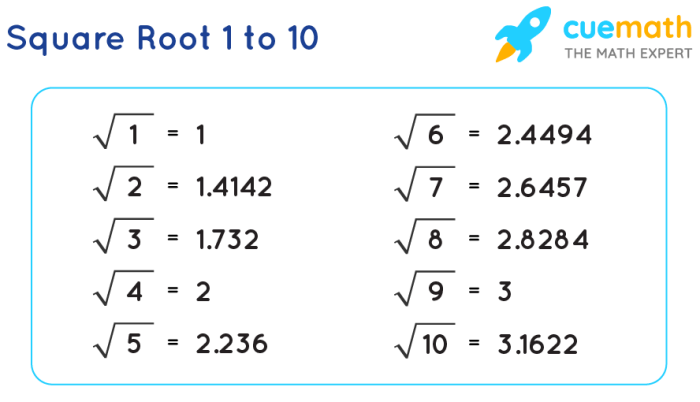Akar dari 6, sebuah konsep matematika yang mungkin tampak sederhana namun menyimpan kekayaan pemahaman yang menarik. Angka ini, yang secara sederhana diwakilkan sebagai √6, muncul dalam berbagai konteks, mulai dari perhitungan geometri sederhana hingga aplikasi kompleks dalam fisika dan teknik. Eksplorasi lebih lanjut akan mengungkap berbagai representasi, metode perhitungan, sifat-sifat matematis, serta penerapannya yang luas.
Dalam uraian berikut, kita akan menyelami dunia akar dari 6, menjelajahi berbagai cara untuk merepresentasikannya, menghitung nilai hampirannya, dan memahami sifat-sifat aljabarnya. Kita juga akan melihat bagaimana akar dari 6 diterapkan dalam berbagai bidang, memberikan gambaran lengkap tentang pentingnya angka ini dalam matematika dan aplikasinya di dunia nyata.
Representasi Akar dari 6
Akar dari 6, dinotasikan sebagai √6, merupakan bilangan irasional, artinya tidak dapat dinyatakan sebagai pecahan sederhana dari dua bilangan bulat. Meskipun demikian, akar dari 6 dapat direpresentasikan dalam beberapa bentuk, masing-masing dengan keunggulan dan keterbatasannya sendiri. Berikut ini akan dibahas berbagai representasi akar dari 6, meliputi representasi desimal, pecahan, dan bentuk radikal, serta visualisasi geometrisnya.
Representasi Desimal, Pecahan, dan Radikal Akar dari 6
Akar dari 6 dapat didekati dengan berbagai tingkat akurasi menggunakan representasi desimal, pecahan, dan bentuk radikal. Representasi desimal memberikan nilai numerik yang mendekati nilai sebenarnya, sementara representasi pecahan memberikan pendekatan rasional. Bentuk radikal, √6, merupakan representasi yang paling tepat secara matematis.
| Representasi | Nilai | Akurasi | Keterangan |
|---|---|---|---|
| Desimal | ≈ 2.4494897 | Tinggi, bergantung pada jumlah desimal | Nilai pendekatan yang terus menerus berubah seiring penambahan angka desimal |
| Pecahan | Tidak ada pecahan sederhana yang tepat | Rendah, hanya pendekatan | Hanya bisa didekati dengan pecahan, misalnya 12/5 = 2.4 |
| Radikal | √6 | Tepat | Representasi yang paling akurat secara matematis |
Visualisasi Geometris Akar dari 6
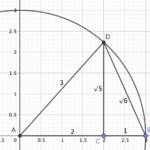
Akar dari 6 dapat divisualisasikan secara geometris dengan membangun sebuah segitiga siku-siku. Misalnya, dengan menggunakan teorema Pythagoras, jika kita memiliki dua sisi segitiga siku-siku dengan panjang 1 dan √5 (yang dapat dibangun dengan segitiga siku-siku lain dengan sisi 1 dan 2), maka sisi miring segitiga tersebut akan memiliki panjang √(1² + (√5)²) = √6. Dengan demikian, panjang sisi miring mewakili nilai akar dari 6 secara visual.
Konstruksi ini dapat dilakukan dengan menggambar garis lurus sepanjang 1 satuan. Kemudian, dari ujung garis tersebut, buatlah garis tegak lurus sepanjang √5 satuan. Hubungkan ujung kedua garis tersebut. Panjang garis penghubung (hipotenusa) akan mewakili √6.
Perbedaan dan Kesamaan Representasi Akar dari 6
Ketiga representasi tersebut memiliki perbedaan utama dalam akurasi dan bentuk penyajian. Representasi radikal (√6) adalah representasi yang paling tepat dan ringkas. Representasi desimal memberikan pendekatan numerik yang dapat bervariasi akurasinya tergantung pada jumlah digit desimal yang digunakan. Sementara representasi pecahan hanya dapat memberikan pendekatan yang kurang akurat.
Kesamaan dari ketiga representasi tersebut adalah semuanya merepresentasikan nilai yang sama, yaitu akar kuadrat dari 6. Mereka hanya berbeda dalam cara penyajian dan tingkat akurasi yang dicapai.
Ilustrasi Hubungan Antar Representasi
Bayangkan sebuah diagram yang menunjukkan √6 sebagai titik pusat. Dari titik tersebut, tiga garis memancar ke arah yang berbeda. Satu garis menuju representasi desimal (misalnya, 2.449), satu garis menuju representasi pecahan (misalnya, 12/5 sebagai pendekatan), dan satu garis menuju representasi radikal (√6). Ketiga garis tersebut menunjukkan bahwa meskipun berbeda dalam bentuk, mereka semua mengarah ke nilai yang sama, yaitu akar kuadrat dari 6.
Panjang setiap garis dapat mewakili tingkat akurasi dari masing-masing representasi, dengan garis menuju representasi radikal memiliki panjang terpendek (menunjukkan akurasi tertinggi).
Perhitungan dan Aproksimasi Akar dari 6
Mencari nilai akar kuadrat dari 6 bukanlah hal yang mudah dilakukan secara manual dengan presisi tinggi. Angka 6 bukanlah bilangan kuadrat sempurna, sehingga akarnya merupakan bilangan irasional, yang artinya memiliki angka desimal tak berujung dan tak berpola. Oleh karena itu, kita perlu menggunakan metode aproksimasi untuk mendapatkan nilai akar dari 6 yang mendekati nilai sebenarnya.
Metode Iteratif Newton-Raphson
Metode Newton-Raphson merupakan salah satu metode iteratif yang efektif untuk mencari akar suatu fungsi. Dalam konteks ini, fungsi yang kita gunakan adalah f(x) = x²
-6, dan kita ingin mencari nilai x yang membuat f(x) =
0. Rumus iterasi Newton-Raphson adalah:
xn+1 = x n
f(xn) / f'(x n)
dimana f'(x) adalah turunan pertama dari f(x). Dalam kasus kita, f'(x) = 2x. Mari kita mulai dengan tebakan awal x 0 = 2.
5. Berikut langkah-langkah perhitungan:
- Iterasi 1: x1 = 2.5 – (2.5²
- 6) / (2
- 2.5) = 2.45
- Iterasi 2: x 2 = 2.45 – (2.45²
- 6) / (2
- 2.45) ≈ 2.44949
- Iterasi 3: x 3 = 2.44949 – (2.44949²
- 6) / (2
- 2.44949) ≈ 2.44948974
Dengan setiap iterasi, nilai x semakin mendekati akar dari 6. Proses ini dapat dilanjutkan hingga mencapai tingkat akurasi yang diinginkan.
Aproksimasi Menggunakan Kalkulator
Cara paling mudah untuk mendapatkan aproksimasi akar dari 6 adalah dengan menggunakan kalkulator atau perangkat lunak matematika. Sebagian besar kalkulator ilmiah akan memberikan hasil sekitar 2.44948974278.
Perbandingan Metode Aproksimasi
- Metode Newton-Raphson: Metode iteratif yang relatif cepat dan akurat, namun membutuhkan pemahaman kalkulus.
- Kalkulator/Perangkat Lunak: Metode yang paling mudah dan cepat, memberikan hasil yang sangat akurat.
- Metode Babilonia (atau Heron): Metode iteratif lain yang relatif sederhana, tetapi konvergensinya lebih lambat dibandingkan Newton-Raphson.
Konsep Galat dalam Perhitungan Aproksimasi
Galat atau error dalam perhitungan aproksimasi mengacu pada perbedaan antara nilai aproksimasi dan nilai sebenarnya. Karena akar dari 6 adalah bilangan irasional, kita tidak dapat menghitung nilai sebenarnya secara tepat. Galat dapat diukur sebagai selisih absolut atau relatif antara nilai aproksimasi dan nilai sebenarnya (yang biasanya didekati dengan nilai yang sangat akurat dari kalkulator). Semakin kecil galat, semakin akurat aproksimasi tersebut.
Contoh Perhitungan Aproksimasi dengan Tingkat Akurasi Berbeda
Dengan menggunakan kalkulator, kita dapat mendapatkan berbagai tingkat akurasi. Misalnya:
- Akurasi 2 desimal: 2.45
- Akurasi 4 desimal: 2.4495
- Akurasi 8 desimal: 2.44948974
Tingkat akurasi yang dibutuhkan bergantung pada konteks permasalahan. Dalam beberapa aplikasi, akurasi 2 desimal sudah cukup, sementara dalam aplikasi lain, akurasi yang lebih tinggi mungkin diperlukan.
Sifat-Sifat Matematis Akar dari 6
Akar dari 6, dinotasikan sebagai √6, merupakan bilangan irasional, artinya tidak dapat dinyatakan sebagai pecahan dari dua bilangan bulat. Meskipun demikian, √6 memiliki sifat-sifat aljabar yang dapat dimanipulasi menggunakan aturan-aturan matematika standar. Pemahaman tentang sifat-sifat ini penting dalam penyederhanaan ekspresi aljabar dan penyelesaian berbagai permasalahan matematika.
Operasi Aljabar pada Akar dari 6
Akar dari 6, seperti bilangan irasional lainnya, dapat terlibat dalam operasi aljabar dasar seperti penjumlahan, pengurangan, perkalian, dan pembagian. Namun, perlu diingat bahwa hasil operasi tersebut tidak selalu menghasilkan bilangan rasional. Berikut beberapa contoh:
- Penjumlahan dan Pengurangan: √6 + 2 tidak dapat disederhanakan lebih lanjut. Begitu pula dengan √6 – 3. Hasilnya tetap berupa ekspresi yang melibatkan √6.
- Perkalian: √6 x 2 = 2√6. Perkalian dengan bilangan rasional hanya mengalikan koefisien dari √6. √6 x √6 = 6, karena perkalian akar kuadrat dengan dirinya sendiri menghasilkan bilangan di dalam akar.
- Pembagian: 6 / √6 = √6. Ini karena 6 dapat ditulis sebagai √36, dan √36 / √6 = √(36/6) = √6.
Penyederhanaan Ekspresi Aljabar yang Melibatkan Akar dari 6
Penyederhanaan ekspresi aljabar yang melibatkan √6 seringkali melibatkan faktorisasi dan pengelompokan suku-suku sejenis. Misalnya, ekspresi 2√6 + 3√6 dapat disederhanakan menjadi 5√6. Ekspresi yang lebih kompleks mungkin memerlukan manipulasi aljabar lebih lanjut sebelum dapat disederhanakan.
Sebagai contoh, perhatikan ekspresi (√6 + 2)(√6 – 2). Dengan menggunakan rumus selisih kuadrat (a+b)(a-b) = a²
-b², kita dapat menyederhanakannya menjadi (√6)²
-2² = 6 – 4 = 2.
Contoh Soal dan Penyelesaiannya
Berikut contoh soal dan penyelesaiannya yang melibatkan operasi matematika pada akar dari 6:
| Soal | Penyelesaian |
|---|---|
| Sederhanakan ekspresi: 3√6 + 5√24 – √54 | Pertama, sederhanakan setiap suku: √24 = √(4 x 6) = 2√6 √54 = √(9 x 6) = 3√6 Maka ekspresi menjadi: 3√6 + 5(2√6) – 3√6 = 3√6 + 10√6 – 3√6 = 10√6 |
| Hitunglah nilai dari (√6 + 2)² | Dengan menggunakan rumus (a+b)² = a² + 2ab + b², kita peroleh: (√6 + 2)² = (√6)² + 2(√6)(2) + 2² = 6 + 4√6 + 4 = 10 + 4√6 |
Rasionalisasi Penyebut yang Mengandung Akar dari 6
Rasionalisasi penyebut bertujuan untuk menghilangkan akar dari penyebut pecahan. Jika penyebut mengandung √6, kita dapat merasionalisasinya dengan mengalikan pembilang dan penyebut dengan √
6. Misalnya, untuk merasionalisasi 1/√6, kita kalikan pembilang dan penyebut dengan √6:
(1/√6) x (√6/√6) = √6/6
Untuk pecahan yang lebih kompleks, seperti (2 + √6) / (3 – √6), kita perlu mengalikan pembilang dan penyebut dengan konjugat penyebut (3 + √6):
[(2 + √6) / (3 – √6)] x [(3 + √6) / (3 + √6)] = (6 + 2√6 + 3√6 + 6) / (9 – 6) = (12 + 5√6) / 3 = 4 + (5/3)√6
Penerapan Akar dari 6

Akar kuadrat dari 6, meskipun tidak sepopuler akar kuadrat dari 2 atau 3, memiliki peran penting dalam berbagai perhitungan matematika dan aplikasi di dunia nyata. Nilai √6, sekitar 2.449, sering muncul dalam permasalahan geometri, fisika, dan teknik, menunjukkan pentingnya memahami dan mengaplikasikannya.
Penerapan Akar dari 6 dalam Geometri
Akar dari 6 seringkali muncul dalam perhitungan panjang diagonal atau sisi pada bangun datar tertentu. Misalnya, pada persegi panjang dengan sisi a dan b, diagonalnya memiliki panjang √(a² + b²). Jika a dan b memiliki nilai tertentu yang menghasilkan a² + b² = 6, maka panjang diagonalnya adalah √6.
Sebagai contoh lain, perhatikan segitiga siku-siku dengan sisi-sisi 1 dan √5. Hipotenusa segitiga ini akan bernilai √(1² + (√5)²) = √6.
Perhitungan Panjang Diagonal Bangun Datar
Perhitungan panjang diagonal bangun datar sering melibatkan akar dari 6. Sebagai contoh, perhatikan sebuah persegi panjang dengan panjang sisi 1 dan √5. Dengan menggunakan teorema Pythagoras, panjang diagonalnya adalah √(1² + (√5)²) = √(1 + 5) = √6. Jadi, akar dari 6 mewakili panjang diagonal persegi panjang tersebut.
Contoh Kasus Penerapan Akar dari 6 dalam Segitiga
Berikut contoh kasus perhitungan panjang sisi segitiga yang melibatkan akar dari 6:
Sebuah segitiga siku-siku memiliki hipotenusa sepanjang √6 dan salah satu sisi siku-sikunya sepanjang 1. Berapakah panjang sisi siku-siku lainnya?
Penyelesaian:
Berdasarkan teorema Pythagoras, a² + b² = c², dimana a dan b adalah sisi siku-siku dan c adalah hipotenusa. Dalam kasus ini, c = √6 dan a =
1. Maka:1² + b² = (√6)²
1 + b² = 6
b² = 5
b = √5
Jadi, panjang sisi siku-siku lainnya adalah √5.
Aplikasi Praktis Akar dari 6 dalam Kehidupan Sehari-hari
Meskipun tidak se-sering akar kuadrat dari 2, aplikasi akar dari 6 dalam kehidupan sehari-hari mungkin kurang terlihat secara langsung. Namun, dalam berbagai perhitungan teknik sipil, desain bangunan, atau bahkan dalam pembuatan kerajinan yang melibatkan geometri presisi, nilai √6 bisa muncul dalam perhitungan jarak, dimensi, atau proporsi.
Peran Akar dari 6 dalam Persamaan Matematika
Akar dari 6 muncul dalam penyelesaian berbagai persamaan matematika, khususnya yang melibatkan persamaan kuadrat atau persamaan yang melibatkan teorema Pythagoras. Sebagai contoh, persamaan x² = 6 memiliki solusi x = ±√6. Begitu juga dalam persamaan yang lebih kompleks yang melibatkan trigonometri atau kalkulus, nilai √6 dapat muncul sebagai bagian dari solusi.
Kesimpulan
Perjalanan kita menjelajahi akar dari 6 telah menunjukkan bahwa meskipun tampak sederhana, angka ini menyimpan kedalaman matematis yang signifikan. Dari berbagai representasinya hingga aplikasinya yang beragam, akar dari 6 membuktikan bahwa bahkan konsep matematika yang paling dasar pun dapat memiliki implikasi yang luas dan mendalam. Pemahaman yang komprehensif tentang akar dari 6, seperti yang telah dibahas, membuka pintu menuju pemahaman yang lebih baik tentang berbagai konsep matematika dan aplikasinya di berbagai disiplin ilmu.