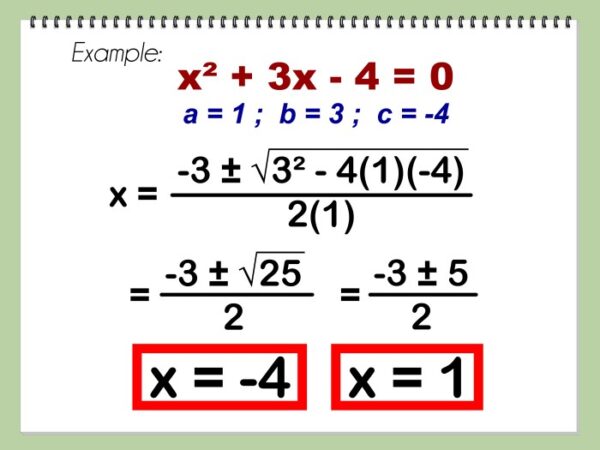Rumus akar persamaan kuadrat merupakan kunci untuk memecahkan berbagai persamaan matematika yang melibatkan variabel berpangkat dua. Memahami rumus ini tidak hanya penting dalam konteks akademis, tetapi juga memiliki aplikasi luas dalam berbagai bidang, mulai dari fisika dan teknik hingga ekonomi dan ilmu komputer. Dengan memahami berbagai metode penyelesaian, seperti rumus umum, pemfaktoran, dan melengkapi kuadrat sempurna, kita dapat menguasai teknik untuk menemukan akar-akar persamaan kuadrat dengan efisien dan akurat.
Artikel ini akan membahas secara detail rumus umum untuk mencari akar-akar persamaan kuadrat (ax² + bx + c = 0), menjelaskan langkah-langkah penyelesaiannya, dan membandingkannya dengan metode alternatif seperti pemfaktoran dan melengkapi kuadrat sempurna. Selain itu, kita juga akan melihat penerapan rumus ini dalam menyelesaikan masalah kontekstual di dunia nyata.
Rumus Umum Akar Persamaan Kuadrat
Persamaan kuadrat merupakan persamaan polinomial berderajat dua yang memiliki bentuk umum ax² + bx + c = 0, di mana a, b, dan c merupakan konstanta dan a ≠ 0. Menemukan akar-akar persamaan kuadrat, yaitu nilai x yang memenuhi persamaan, sangat penting dalam berbagai aplikasi matematika dan ilmu terapan. Rumus umum yang digunakan untuk mencari akar-akar ini memberikan solusi yang efisien dan akurat.
Rumus umum untuk mencari akar-akar persamaan kuadrat ax² + bx + c = 0 adalah sebagai berikut:
x = [-b ± √(b²
4ac)] / 2a
Rumus ini dikenal juga sebagai rumus kuadratik. Bagian b²
-4ac disebut diskriminan (D), yang menentukan jenis akar-akar persamaan kuadrat.
Penerapan Rumus pada Persamaan Kuadrat 2x² + 5x + 3 = 0
Mari kita terapkan rumus umum tersebut pada persamaan kuadrat 2x² + 5x + 3 =
0. Dalam persamaan ini, a = 2, b = 5, dan c =
3. Substitusikan nilai-nilai ini ke dalam rumus:
x = [-5 ± √(5²
-4
– 2
– 3)] / (2
– 2)
x = [-5 ± √(25 – 24)] / 4
x = [-5 ± √1] / 4
x = [-5 ± 1] / 4
Kita memperoleh dua akar:
x₁ = (-5 + 1) / 4 = -1
x₂ = (-5 – 1) / 4 = -3/2 = -1.5
Jadi, akar-akar persamaan kuadrat 2x² + 5x + 3 = 0 adalah x = -1 dan x = -1.5.
Contoh Persamaan Kuadrat dan Akar-akarnya
Berikut tabel yang menunjukkan koefisien dan akar-akar dari tiga contoh persamaan kuadrat berbeda. Tabel ini dirancang responsif untuk tampilan yang optimal di berbagai perangkat.
| Koefisien a | Koefisien b | Koefisien c | Akar-akar Persamaan |
|---|---|---|---|
| 1 | -5 | 6 | x = 2, x = 3 |
| 2 | -7 | 3 | x = 3, x = 1/2 |
| 1 | 2 | 1 | x = -1 |
Contoh Persamaan Kuadrat dengan Akar-akar Real dan Berbeda
Perhatikan persamaan kuadrat x²
-5x + 6 =
0. Dalam persamaan ini, a = 1, b = -5, dan c =
6. Dengan menggunakan rumus umum:
x = [5 ± √((-5)²
-4
– 1
– 6)] / (2
– 1)
x = [5 ± √(25 – 24)] / 2
x = [5 ± √1] / 2
x = [5 ± 1] / 2
Akar-akarnya adalah x₁ = 3 dan x₂ = 2. Kedua akar ini merupakan bilangan real dan berbeda.
Kondisi Diskriminan (D = b² – 4ac)
Diskriminan (D = b²
-4ac) memberikan informasi tentang jenis akar-akar persamaan kuadrat:
- Jika D > 0, maka persamaan kuadrat memiliki dua akar real yang berbeda.
- Jika D = 0, maka persamaan kuadrat memiliki dua akar real yang sama (akar kembar).
- Jika D < 0, maka persamaan kuadrat memiliki dua akar imajiner (kompleks).
Metode Pemfaktoran
Metode pemfaktoran merupakan salah satu cara efektif untuk mencari akar-akar persamaan kuadrat, terutama jika persamaan tersebut dapat difaktorkan dengan mudah. Metode ini didasarkan pada sifat perkalian nol, yaitu jika perkalian dua bilangan sama dengan nol, maka salah satu atau kedua bilangan tersebut haruslah nol. Dengan memfaktorkan persamaan kuadrat, kita dapat mengubahnya menjadi bentuk perkalian dua faktor, sehingga kita dapat menentukan nilai x yang membuat hasil perkalian tersebut sama dengan nol.
Metode ini menawarkan pendekatan yang lebih intuitif dan seringkali lebih cepat dibandingkan dengan rumus kuadrat umum, khususnya untuk persamaan kuadrat tertentu.
Contoh Penyelesaian Persamaan Kuadrat dengan Metode Pemfaktoran
Mari kita selesaikan persamaan kuadrat x² + 5x + 6 = 0 menggunakan metode pemfaktoran. Langkah-langkahnya adalah sebagai berikut:
- Faktorkan persamaan kuadrat tersebut. Kita mencari dua bilangan yang jika dijumlahkan hasilnya 5 dan jika dikalikan hasilnya 6. Bilangan tersebut adalah 2 dan 3.
- Persamaan kuadrat dapat difaktorkan menjadi (x + 2)(x + 3) = 0.
- Terapkan sifat perkalian nol: (x + 2) = 0 atau (x + 3) = 0.
- Selesaikan masing-masing persamaan: x = -2 atau x = -3.
- Jadi, akar-akar persamaan kuadrat x² + 5x + 6 = 0 adalah x = -2 dan x = -3.
Perbandingan Metode Pemfaktoran dan Rumus Kuadrat Umum
Baik metode pemfaktoran maupun rumus kuadrat umum (rumus abc) digunakan untuk mencari akar-akar persamaan kuadrat. Namun, keduanya memiliki kelebihan dan kekurangan masing-masing.
| Metode | Kelebihan | Kekurangan |
|---|---|---|
| Pemfaktoran | Relatif lebih cepat dan mudah jika persamaan mudah difaktorkan; pendekatan lebih intuitif. | Tidak semua persamaan kuadrat dapat difaktorkan dengan mudah; terkadang sulit menemukan faktor-faktor yang tepat. |
| Rumus Kuadrat Umum | Dapat digunakan untuk menyelesaikan semua jenis persamaan kuadrat, termasuk yang tidak dapat difaktorkan dengan mudah. | Lebih rumit dan membutuhkan perhitungan yang lebih banyak; potensi kesalahan perhitungan lebih tinggi. |
Contoh Persamaan Kuadrat yang Hanya Dapat Diselesaikan dengan Metode Pemfaktoran
Meskipun tidak selalu mudah untuk menentukan persamaan mana yang hanya dapat diselesaikan dengan pemfaktoran, persamaan seperti x²
-4 = 0 lebih mudah diselesaikan dengan pemfaktoran (x-2)(x+2) = 0, menghasilkan akar x = 2 dan x = -2. Mencoba menyelesaikannya dengan rumus kuadrat umum akan lebih panjang dan rumit, meskipun menghasilkan hasil yang sama.
Metode pemfaktoran lebih efektif dibandingkan dengan rumus kuadrat umum ketika persamaan kuadrat dapat difaktorkan dengan mudah dan cepat. Hal ini akan menghemat waktu dan usaha dalam perhitungan. Namun, jika persamaan sulit difaktorkan atau tidak dapat difaktorkan sama sekali, maka rumus kuadrat umum menjadi pilihan yang lebih tepat.
Metode Melengkapkan Kuadrat Sempurna
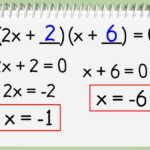
Metode melengkapi kuadrat sempurna merupakan salah satu teknik aljabar yang efektif untuk mencari akar-akar persamaan kuadrat. Metode ini mengubah bentuk umum persamaan kuadrat menjadi bentuk kuadrat sempurna, sehingga akar-akarnya dapat ditemukan dengan mudah. Keunggulan metode ini terletak pada kemampuannya untuk menyelesaikan persamaan kuadrat yang sulit difaktorkan secara langsung.
Secara umum, metode ini melibatkan manipulasi aljabar untuk mengubah persamaan kuadrat ax² + bx + c = 0 menjadi bentuk (x + p)² = q, di mana p dan q merupakan konstanta. Dari bentuk ini, akar-akar persamaan dapat langsung ditentukan.
Langkah-langkah Melengkapi Kuadrat Sempurna
Berikut langkah-langkah umum dalam menyelesaikan persamaan kuadrat dengan metode melengkapi kuadrat sempurna:
- Pastikan koefisien dari x² adalah 1. Jika tidak, bagi seluruh persamaan dengan koefisien x².
- Pindahkan konstanta (suku tanpa variabel x) ke ruas kanan persamaan.
- Tentukan setengah dari koefisien x (b/2a), lalu kuadratkan hasilnya ((b/2a)²).
- Tambahkan hasil kuadrat tersebut ke kedua ruas persamaan. Ini akan membentuk kuadrat sempurna di ruas kiri.
- Faktorkan ruas kiri menjadi bentuk (x + p)².
- Akar kuadratkan kedua ruas persamaan.
- Selesaikan persamaan untuk mencari nilai x.
Contoh Penyelesaian Persamaan Kuadrat dengan Metode Melengkapi Kuadrat Sempurna
Mari kita selesaikan persamaan kuadrat x² + 6x + 8 = 0 dengan metode melengkapi kuadrat sempurna:
- Koefisien x² sudah 1, jadi langkah ini tidak perlu dilakukan.
- Pindahkan konstanta ke ruas kanan: x² + 6x = -8
- Setengah dari koefisien x (6) adalah 3, dan kuadratnya adalah 9.
- Tambahkan 9 ke kedua ruas: x² + 6x + 9 = -8 + 9
- Faktorkan ruas kiri: (x + 3)² = 1
- Akar kuadratkan kedua ruas: x + 3 = ±1
- Selesaikan untuk x:
- x + 3 = 1 => x = -2
- x + 3 = -1 => x = -4
Jadi, akar-akar persamaan x² + 6x + 8 = 0 adalah x = -2 dan x = -4.
Perbandingan Metode Melengkapi Kuadrat Sempurna dengan Metode Lain
Metode melengkapi kuadrat sempurna, pemfaktoran, dan rumus kuadrat umum semuanya dapat digunakan untuk menyelesaikan persamaan kuadrat. Metode pemfaktoran paling efisien jika persamaan mudah difaktorkan. Rumus kuadrat umum selalu dapat digunakan, tetapi rumusnya lebih kompleks. Metode melengkapi kuadrat sempurna menjadi pilihan yang baik ketika persamaan kuadrat sulit difaktorkan secara langsung, tetapi masih relatif lebih mudah dipahami daripada rumus kuadrat umum.
Contoh Soal yang Lebih Kompleks
Selesaikan persamaan kuadrat 2x²
-8x + 5 = 0 menggunakan metode melengkapi kuadrat sempurna.
- Bagi seluruh persamaan dengan 2: x² – 4x + 5/2 = 0
- Pindahkan konstanta ke ruas kanan: x²
4x = -5/2
- Setengah dari koefisien x (-4) adalah -2, dan kuadratnya adalah 4.
- Tambahkan 4 ke kedua ruas: x²
4x + 4 = -5/2 + 4
- Faktorkan ruas kiri: (x – 2)² = 3/2
- Akar kuadratkan kedua ruas: x – 2 = ±√(3/2)
- Selesaikan untuk x: x = 2 ± √(3/2)
Penerapan dalam Masalah Kontekstual

Rumus akar persamaan kuadrat bukan hanya sekadar rumus matematis abstrak. Kegunaannya meluas ke berbagai bidang, membantu memecahkan masalah dunia nyata yang kompleks. Memahami penerapannya memungkinkan kita untuk memodelkan dan menyelesaikan permasalahan yang awalnya tampak rumit menjadi langkah-langkah terstruktur dan terukur.
Berikut ini akan dijelaskan langkah-langkah menerjemahkan soal cerita ke dalam persamaan kuadrat, disertai contoh soal dan penyelesaiannya. Selain itu, akan disajikan pula contoh soal lain untuk memperkaya pemahaman.
Contoh Soal Cerita dan Penyelesaiannya, Rumus akar persamaan kuadrat
Sebuah taman berbentuk persegi panjang memiliki luas 100 m². Panjang taman 5 meter lebih panjang dari lebarnya. Tentukan panjang dan lebar taman tersebut.
- Menerjemahkan ke dalam Persamaan Kuadrat: Misalkan lebar taman adalah x meter. Maka panjang taman adalah (x + 5) meter. Luas taman adalah panjang kali lebar, sehingga kita peroleh persamaan: x(x + 5) = 100.
- Penyederhanaan Persamaan: Persamaan di atas dapat disederhanakan menjadi x² + 5x – 100 = 0.
- Mencari Akar Persamaan Kuadrat: Kita dapat menggunakan rumus akar persamaan kuadrat untuk mencari nilai x:
x = [-b ± √(b²4ac)] / 2a
Dengan a = 1, b = 5, dan c = -100. Setelah dihitung, kita akan mendapatkan dua nilai x, yaitu x = 8 dan x = -12.5. - Interpretasi Hasil: Karena x mewakili lebar taman, nilai x yang negatif (-12.5) tidak masuk akal. Oleh karena itu, lebar taman adalah 8 meter. Panjang taman adalah x + 5 = 8 + 5 = 13 meter.
Contoh Soal Cerita Tambahan 1
Sebuah roket diluncurkan vertikal ke atas. Tinggi roket (dalam meter) setelah t detik diberikan oleh persamaan h(t) = -5t² + 20t + 10. Tentukan waktu yang dibutuhkan roket untuk mencapai ketinggian 25 meter.
- Kita substitusikan h(t) = 25 ke dalam persamaan: 25 = -5t² + 20t + 10.
- Kemudian kita sederhanakan persamaan menjadi: 5t²
- 20t + 15 = 0, atau t²
- 4t + 3 = 0.
- Dengan menggunakan rumus kuadrat atau pemfaktoran, kita peroleh t = 1 dan t = 3. Ini berarti roket mencapai ketinggian 25 meter pada detik ke-1 dan detik ke-3 (saat naik dan saat turun).
Contoh Soal Cerita Tambahan 2
Sebuah petani ingin membuat kandang ayam berbentuk persegi panjang dengan luas 50 m². Ia hanya memiliki kawat sepanjang 30 meter untuk pagar. Tentukan panjang dan lebar kandang ayam tersebut.
- Misalkan panjang kandang adalah p dan lebarnya l. Luas kandang adalah pl = 50, dan kelilingnya 2(p+l) = 30, sehingga p + l = 15 atau p = 15 – l.
- Substitusikan p ke persamaan luas: (15-l)l = 50, yang disederhanakan menjadi l² – 15l + 50 = 0.
- Dengan menggunakan rumus kuadrat, kita peroleh l = 5 atau l = 10. Jika l = 5, maka p = 10. Jika l = 10, maka p = 5.
- Jadi, panjang dan lebar kandang ayam adalah 10 meter dan 5 meter.
Pemahaman yang mendalam tentang akar persamaan kuadrat sangat penting dalam memecahkan berbagai masalah dunia nyata, mulai dari perencanaan konstruksi dan perhitungan lintasan proyektil hingga analisis data ekonomi dan model pertumbuhan populasi. Kemampuan untuk menerjemahkan masalah kontekstual ke dalam model matematika dan menyelesaikannya dengan tepat sangat berharga dalam berbagai disiplin ilmu.
Kesimpulan: Rumus Akar Persamaan Kuadrat
Memahami rumus akar persamaan kuadrat dan berbagai metode penyelesaiannya membuka pintu bagi pemahaman yang lebih dalam tentang matematika dan aplikasinya. Kemampuan untuk mengaplikasikan rumus ini tidak hanya terbatas pada soal-soal matematika saja, tetapi juga membantu dalam menyelesaikan masalah-masalah kompleks di berbagai disiplin ilmu. Dengan latihan yang cukup, Anda akan mampu dengan percaya diri menangani berbagai jenis persamaan kuadrat dan mengaplikasikannya dalam konteks yang lebih luas.