Akar 1, atau akar pangkat satu, mungkin terdengar sederhana, namun pemahamannya mendasari banyak konsep matematika dan aplikasinya dalam kehidupan sehari-hari. Konsep ini, yang secara matematis didefinisikan sebagai bilangan yang jika dipangkatkan satu hasilnya adalah bilangan itu sendiri, terlihat sepele, tetapi perannya krusial dalam berbagai bidang, dari persamaan matematika hingga ilmu komputer. Mari kita telusuri lebih dalam tentang akar 1 dan aplikasinya yang luas.
Artikel ini akan menjelaskan secara detail pengertian akar pangkat satu, membandingkannya dengan pangkat dua dan tiga, serta menunjukkan penerapannya dalam persamaan matematika, representasi grafis, dan berbagai bidang seperti teknik, fisika, dan ilmu komputer. Dengan contoh-contoh yang jelas dan ilustrasi yang mudah dipahami, diharapkan pembaca dapat menguasai konsep akar 1 dengan baik.
Konsep Akar 1
Akar pangkat satu, meskipun tampak sederhana, merupakan konsep dasar dalam matematika yang seringkali terlupakan karena kesederhanaannya. Pemahaman yang kuat tentang akar pangkat satu menjadi fondasi untuk memahami operasi matematika yang lebih kompleks. Artikel ini akan menguraikan konsep akar pangkat satu, membandingkannya dengan pangkat lain, dan menunjukkan penerapannya dalam kehidupan sehari-hari.
Pengertian Akar Pangkat Satu
Secara matematis, akar pangkat satu dari suatu bilangan adalah bilangan itu sendiri. Dengan kata lain, mencari akar pangkat satu dari sebuah angka sama saja dengan angka tersebut. Operasi ini dilambangkan dengan 1√x = x, di mana x mewakili bilangan real. Hal ini berbeda dengan akar pangkat dua atau tiga yang membutuhkan proses perhitungan lebih lanjut.
Contoh Perhitungan Akar Pangkat Satu
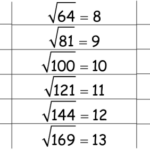
Perhitungan akar pangkat satu sangatlah mudah. Misalnya, akar pangkat satu dari 5 adalah 5 ( 1√5 = 5), akar pangkat satu dari 100 adalah 100 ( 1√100 = 100), dan seterusnya. Tidak ada proses perhitungan yang rumit karena hasilnya langsung sama dengan bilangan yang diawali.
Perbandingan Akar Pangkat Satu, Dua, dan Tiga
Tabel berikut membandingkan akar pangkat satu, dua, dan tiga, menunjukkan perbedaan mendasar dalam perhitungan dan hasilnya.
| Pangkat | Rumus | Contoh | Hasil |
|---|---|---|---|
| Satu | 1√x = x | 1√9 | 9 |
| Dua | √x | √9 | 3 |
| Tiga | 3√x | 3√27 | 3 |
Perbedaan Akar Pangkat Satu dengan Operasi Matematika Lainnya
Akar pangkat satu berbeda secara signifikan dengan operasi matematika lainnya seperti penjumlahan, pengurangan, perkalian, dan pembagian. Operasi-operasi tersebut mengubah nilai bilangan awal, sedangkan akar pangkat satu mempertahankan nilai bilangan tersebut. Perbedaan ini menjadi kunci dalam memahami bagaimana akar pangkat satu digunakan dalam konteks yang lebih luas.
Penerapan Akar Pangkat Satu dalam Kehidupan Sehari-hari
Meskipun terlihat sederhana, akar pangkat satu memiliki implikasi praktis. Misalnya, jika kita memiliki 10 apel dan kita ingin membagi apel tersebut menjadi 1 bagian, maka jumlah apel di setiap bagian adalah 1√10 = 10 apel. Konsep ini diterapkan secara implisit dalam berbagai situasi sehari-hari di mana kita menghitung jumlah total suatu objek tanpa perlu pembagian atau pengelompokan lebih lanjut.
Akar 1 dalam Persamaan Matematika
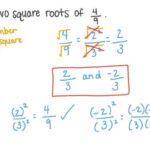
Akar pangkat satu, atau yang lebih dikenal sebagai akar kuadrat, merupakan operasi matematika dasar yang sering dijumpai dalam berbagai persamaan. Memahami cara menyelesaikan persamaan yang melibatkan akar pangkat satu sangat penting dalam berbagai bidang, mulai dari aljabar dasar hingga aplikasi matematika yang lebih kompleks dalam ilmu fisika dan teknik.
Contoh Persamaan Sederhana yang Melibatkan Akar Pangkat Satu
Persamaan sederhana yang melibatkan akar pangkat satu biasanya dapat diselesaikan dengan operasi aljabar dasar. Sebagai contoh, perhatikan persamaan berikut: √x = 5. Untuk menyelesaikan persamaan ini, kita cukup mengkuadratkan kedua ruas persamaan. Dengan demikian, kita peroleh x = 25. Penyelesaian ini relatif mudah karena persamaan hanya melibatkan satu operasi akar pangkat satu.
Contoh Persamaan Kompleks yang Melibatkan Akar Pangkat Satu dan Operasi Matematika Lain
Persamaan yang lebih kompleks melibatkan akar pangkat satu dan operasi matematika lain seperti penjumlahan, pengurangan, perkalian, dan pembagian. Keberadaan operasi lain ini menuntut strategi penyelesaian yang lebih sistematis.
Sebagai ilustrasi, perhatikan persamaan berikut:
2√(x + 3) + 5 = 11
Penyelesaian persamaan ini membutuhkan langkah-langkah berikut:
- Kurangi 5 dari kedua ruas: 2√(x + 3) = 6
- Bagi kedua ruas dengan 2: √(x + 3) = 3
- Kuadratkan kedua ruas: x + 3 = 9
- Kurangi 3 dari kedua ruas: x = 6
Dengan demikian, solusi dari persamaan tersebut adalah x = 6. Perlu diperhatikan bahwa ketika mengkuadratkan kedua ruas persamaan yang melibatkan akar, kita perlu memeriksa kembali solusi yang diperoleh untuk memastikan bahwa solusi tersebut valid dan tidak menghasilkan nilai negatif di dalam akar.
Pengaruh Akar Pangkat Satu terhadap Solusi Persamaan
Akar pangkat satu dalam suatu persamaan dapat membatasi domain solusi, karena nilai di dalam akar tidak boleh negatif. Ini berarti bahwa solusi persamaan haruslah nilai yang membuat ekspresi di dalam akar bernilai non-negatif. Jika solusi yang diperoleh menghasilkan nilai negatif di dalam akar, maka solusi tersebut harus ditolak. Proses pengecekan ini penting untuk memastikan keakuratan solusi.
Representasi Akar 1 secara Grafis
Akar pangkat satu dari suatu bilangan, yang secara sederhana adalah bilangan itu sendiri, memiliki representasi grafis yang unik dan sederhana jika dibandingkan dengan fungsi pangkat lainnya. Representasi ini memberikan pemahaman visual tentang hubungan antara nilai numerik dan representasi geometriknya pada bidang koordinat Kartesius.
Grafik Akar Pangkat Satu pada Bidang Koordinat Kartesius
Grafik akar pangkat satu (y = √x, atau lebih tepatnya y = x jika kita hanya membahas akar pangkat satu dari bilangan positif) pada bidang koordinat Kartesius berupa garis lurus yang melewati titik asal (0,0) dan memiliki kemiringan 45 derajat terhadap sumbu x positif. Setiap titik pada garis ini merepresentasikan pasangan terurut (x,y) di mana y adalah akar pangkat satu dari x (atau y = x).
Garis ini hanya berada di kuadran I (x ≥ 0, y ≥ 0) karena kita hanya mempertimbangkan akar kuadrat dari bilangan riil non-negatif.
Hubungan Representasi Grafis dan Nilai Numerik Akar Pangkat Satu
Hubungan antara representasi grafis dan nilai numerik sangat langsung. Setiap titik pada garis mewakili pasangan (x, x), menunjukkan bahwa nilai y selalu sama dengan nilai x. Misalnya, titik (2, 2) menunjukkan bahwa akar pangkat satu dari 2 adalah 2. Semakin besar nilai x, semakin jauh titik tersebut dari titik asal, menunjukkan peningkatan nilai akar pangkat satu secara linier.
Perbandingan dengan Representasi Grafis Fungsi Pangkat Lain
Berbeda dengan grafik fungsi kuadrat (y = x²) yang berbentuk parabola, atau fungsi pangkat tiga (y = x³) yang berbentuk kurva yang lebih kompleks, grafik akar pangkat satu sangat sederhana, yaitu berupa garis lurus. Grafik fungsi kuadrat dan pangkat tiga menunjukkan hubungan non-linier antara x dan y, sedangkan grafik akar pangkat satu menunjukkan hubungan linier yang sederhana dan langsung.
Pengaruh Perubahan Nilai terhadap Representasi Grafis
Perubahan nilai x secara langsung memengaruhi posisi titik pada garis. Jika nilai x diperbesar, titik akan bergeser ke kanan dan ke atas sepanjang garis dengan jarak yang sama. Jika nilai x diperkecil, titik akan bergeser ke kiri dan ke bawah. Ini menunjukkan bahwa perubahan nilai x menghasilkan perubahan nilai y yang proporsional dan linier.
Interpretasi Ilustrasi, Akar 1
Ilustrasi grafik akar pangkat satu memberikan gambaran visual yang jelas tentang sifat linier dari fungsi ini. Kemiringan garis yang konstan pada 45 derajat menunjukkan hubungan proporsionalitas langsung antara x dan y. Kehadiran grafik ini memudahkan pemahaman tentang hubungan antara nilai numerik dan representasi geometrik dari akar pangkat satu, memberikan pemahaman yang lebih intuitif dibandingkan hanya dengan melihat persamaan aljabarnya.
Aplikasi Akar 1 di Berbagai Bidang
Akar pangkat satu, atau lebih dikenal sebagai akar kuadrat, seringkali dianggap sebagai operasi matematika dasar. Namun, penerapannya melampaui ruang lingkup matematika murni dan berperan penting dalam berbagai bidang ilmu pengetahuan dan teknologi. Pemahaman tentang akar pangkat satu menjadi krusial dalam menyelesaikan berbagai permasalahan praktis di berbagai disiplin ilmu.
Aplikasi Akar Pangkat Satu di Bidang Teknik
Dalam teknik sipil, misalnya, perhitungan panjang diagonal suatu bidang persegi atau persegi panjang menggunakan teorema Pythagoras membutuhkan penggunaan akar kuadrat. Akar kuadrat juga digunakan dalam perhitungan tegangan dan regangan pada material, memastikan struktur bangunan aman dan kokoh. Pada teknik elektro, akar kuadrat digunakan dalam perhitungan impedansi dan daya listrik, membantu dalam mendesain rangkaian listrik yang efisien dan handal.
Contohnya, dalam perhitungan arus listrik bolak-balik (AC), akar kuadrat digunakan untuk menghitung nilai efektif arus.
Aplikasi Akar Pangkat Satu di Bidang Fisika
Konsep akar kuadrat sangat penting dalam berbagai rumus fisika. Sebagai contoh, dalam mekanika, kecepatan suatu objek dapat dihitung menggunakan rumus yang melibatkan akar kuadrat dari energi kinetiknya. Dalam fisika nuklir, akar kuadrat digunakan dalam perhitungan energi partikel subatomik. Di bidang optik, penggunaan akar kuadrat muncul dalam perhitungan indeks bias dan pembiasan cahaya. Contoh sederhana adalah menghitung kecepatan rambat gelombang berdasarkan panjang gelombang dan frekuensi, yang melibatkan akar kuadrat dari konstanta.
Aplikasi Akar Pangkat Satu di Ilmu Komputer
Akar pangkat satu memiliki peran penting dalam algoritma dan struktur data di ilmu komputer. Misalnya, dalam pencarian data pada struktur data seperti pohon pencarian biner, perhitungan kompleksitas waktu seringkali melibatkan akar kuadrat dari jumlah data. Selain itu, penggunaan akar kuadrat juga ditemukan dalam algoritma grafis komputer, seperti perhitungan jarak antara titik-titik pada layar atau dalam pemrosesan gambar.
Tabel Ringkasan Aplikasi Akar Pangkat Satu
| Bidang | Deskripsi | Contoh |
|---|---|---|
| Teknik Sipil | Perhitungan panjang diagonal, tegangan, dan regangan pada struktur. | Menghitung panjang diagonal balok beton menggunakan teorema Pythagoras. |
| Teknik Elektro | Perhitungan impedansi, daya listrik, dan nilai efektif arus AC. | Menghitung impedansi total pada rangkaian seri resistor dan kapasitor. |
| Fisika | Perhitungan kecepatan, energi, dan berbagai besaran fisika lainnya. | Menghitung kecepatan suatu benda berdasarkan energi kinetiknya. |
| Ilmu Komputer | Analisis kompleksitas algoritma, pemrosesan gambar, dan grafis komputer. | Menghitung waktu pencarian data pada pohon pencarian biner. |
Skenario Aplikasi Akar Pangkat Satu dalam Kehidupan Sehari-hari
Bayangkan Anda ingin membuat taman berbentuk persegi dengan luas 100 meter persegi. Untuk mengetahui panjang sisi taman tersebut, Anda perlu menghitung akar kuadrat dari 100, yang hasilnya adalah 10 meter. Ini adalah contoh sederhana bagaimana akar kuadrat digunakan untuk menyelesaikan masalah praktis dalam kehidupan sehari-hari, meskipun mungkin tidak selalu disadari.
Pemungkas: Akar 1
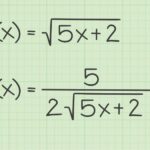
Akar 1, meskipun tampak sederhana, memiliki peran yang signifikan dalam berbagai aspek matematika dan aplikasinya. Memahami konsep ini dengan baik menjadi fondasi untuk mempelajari konsep matematika yang lebih kompleks. Dari persamaan sederhana hingga aplikasi di berbagai bidang, akar 1 menunjukkan betapa konsep matematika yang fundamental dapat memiliki dampak yang luas dan penting. Semoga pemahaman yang telah diuraikan dalam artikel ini dapat bermanfaat bagi pembaca.