
Keliling lingkaran yang memiliki jari-jari 10 cm adalah sebuah perhitungan dasar dalam geometri. Memahami konsep ini membuka pintu untuk menyelesaikan berbagai permasalahan yang melibatkan lingkaran, dari menghitung panjang lintasan hingga mendesain objek melingkar. Perhitungan keliling ini sangat penting dalam berbagai bidang, mulai dari teknik sipil hingga desain grafis.
Rumus keliling lingkaran, yaitu 2πr (dimana r adalah jari-jari), akan kita terapkan untuk menghitung keliling lingkaran dengan jari-jari 10 cm. Kita akan melihat langkah-langkah perhitungan secara detail, termasuk pilihan nilai π (pi) yang berpengaruh pada hasil akhir. Selanjutnya, kita akan menjelajahi aplikasi praktis dari perhitungan keliling lingkaran dalam kehidupan sehari-hari.
Rumus Keliling Lingkaran
Keliling lingkaran merupakan panjang total garis lengkung yang membentuk lingkaran. Memahami cara menghitung keliling lingkaran sangat penting dalam berbagai bidang, mulai dari matematika dasar hingga aplikasi di teknik dan desain.
Rumus keliling lingkaran didasarkan pada hubungan antara jari-jari atau diameter lingkaran dengan panjang kelilingnya. Pemahaman yang baik tentang rumus ini akan memudahkan kita dalam menyelesaikan berbagai permasalahan yang berkaitan dengan lingkaran.
Rumus Keliling Lingkaran dan Variabelnya
Rumus keliling lingkaran dinyatakan sebagai:
K = 2πr
di mana:
- K mewakili keliling lingkaran.
- r mewakili jari-jari lingkaran (jarak dari pusat lingkaran ke titik di lingkaran).
- π (pi) adalah konstanta matematika dengan nilai pendekatan 3.14159 atau 22/7.
Rumus ini menunjukkan bahwa keliling lingkaran berbanding lurus dengan jari-jarinya. Semakin besar jari-jari, semakin besar pula kelilingnya.
Contoh Perhitungan Keliling Lingkaran
Berikut beberapa contoh perhitungan keliling lingkaran dengan jari-jari berbeda:
| Jari-jari (cm) | Rumus | Perhitungan | Hasil Keliling (cm) |
|---|---|---|---|
| 5 | K = 2πr | K = 2
|
31.4159 |
| 10 | K = 2πr | K = 2
|
62.8318 |
| 15 | K = 2πr | K = 2
|
94.2477 |
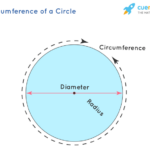
Ilustrasi Lingkaran dengan Jari-jari 10 cm
Bayangkan sebuah lingkaran sempurna dengan jari-jari 10 cm. Pusat lingkaran berada di tengah. Keliling lingkaran tersebut mewakili jarak total yang ditempuh jika kita berjalan mengelilingi lingkaran tersebut tepat di tepiannya. Setiap titik di sepanjang garis lengkung tersebut berjarak 10 cm dari pusat lingkaran. Garis lengkung yang membentuk lingkaran inilah yang disebut keliling.
Rumus Keliling Lingkaran jika Diketahui Diameter
Diameter (d) lingkaran adalah dua kali jari-jari (r), atau d = 2r. Oleh karena itu, rumus keliling lingkaran dapat juga dinyatakan dalam bentuk diameter:
K = πd
Rumus ini memberikan cara alternatif untuk menghitung keliling lingkaran jika kita hanya mengetahui diameternya.
Penerapan Rumus pada Jari-jari 10 cm
Setelah memahami rumus keliling lingkaran, mari kita terapkan pada contoh konkret. Kita akan menghitung keliling lingkaran dengan jari-jari 10 cm, memperhatikan penggunaan nilai π yang berbeda dan menganalisis perbedaan hasilnya. Selanjutnya, akan disajikan pula contoh soal cerita yang relevan.
Perhitungan Keliling Lingkaran dengan Jari-jari 10 cm
Rumus keliling lingkaran adalah K = 2πr, di mana K adalah keliling, π (pi) adalah konstanta matematika, dan r adalah jari-jari lingkaran. Dengan jari-jari 10 cm, perhitungannya sebagai berikut:
- Substitusikan nilai r = 10 cm ke dalam rumus: K = 2π(10 cm)
- Sederhanakan persamaan: K = 20π cm
Langkah selanjutnya adalah menentukan nilai π yang akan digunakan. Penggunaan nilai π bergantung pada tingkat akurasi yang dibutuhkan.
Nilai Pi (π) yang Digunakan
Nilai π adalah konstanta yang merepresentasikan rasio antara keliling lingkaran dengan diameternya. Nilai π bersifat irasional, artinya memiliki angka desimal yang tak berujung dan tak berpola. Dalam perhitungan praktis, kita sering menggunakan pendekatan nilai π dengan angka desimal tertentu, seperti 3.14 atau pecahan 22/7. Penggunaan 3.14 merupakan pendekatan yang umum digunakan karena kesederhanaannya, sementara 22/7 memberikan tingkat akurasi yang sedikit lebih tinggi.
Contoh Soal Cerita
Sebuah taman berbentuk lingkaran memiliki jari-jari 10 meter. Berapa meter pagar yang dibutuhkan untuk mengelilingi taman tersebut?
Solusi Soal Cerita, Keliling lingkaran yang memiliki jari-jari 10 cm adalah
Soal ini menanyakan keliling taman berbentuk lingkaran. Kita gunakan rumus keliling lingkaran K = 2πr dengan r = 10 meter.
- Dengan π ≈ 3.14: K = 2
- 3.14
- 10 m = 62.8 m
- Dengan π ≈ 22/7: K = 2
- (22/7)
- 10 m ≈ 62.86 m
Jadi, dibutuhkan sekitar 62.8 meter pagar jika menggunakan π ≈ 3.14, dan sekitar 62.86 meter jika menggunakan π ≈ 22/7.
Perbandingan Hasil Perhitungan
| Nilai π | Perhitungan | Hasil (meter) |
|---|---|---|
| 3.14 | 2
|
62.8 |
| 22/7 | 2
|
≈ 62.86 |
Perbedaan hasil perhitungan antara menggunakan π = 3.14 dan π = 22/7 relatif kecil pada contoh ini (sekitar 0.06 meter). Namun, perbedaan ini dapat menjadi signifikan jika jari-jari lingkaran jauh lebih besar.
Konsep Keliling dan Luas Lingkaran
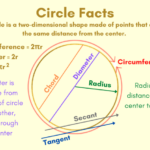
Lingkaran, bentuk geometris yang sederhana namun elegan, memiliki dua karakteristik utama yang sering dihitung: keliling dan luas. Pemahaman yang mendalam tentang keduanya sangat penting dalam berbagai aplikasi praktis, mulai dari perencanaan konstruksi hingga perhitungan dalam ilmu fisika.
Keliling dan luas lingkaran, meskipun keduanya berkaitan dengan lingkaran, menunjukkan aspek yang berbeda. Keliling mengacu pada panjang total garis lengkung yang membentuk lingkaran, sedangkan luas mengacu pada area yang dilingkupi oleh lingkaran tersebut. Perbedaan ini mendasar dan memengaruhi cara kita mengaplikasikan rumus masing-masing dalam pemecahan masalah.
Perbedaan Keliling dan Luas Lingkaran
Perbedaan mendasar antara keliling dan luas lingkaran terletak pada satuannya. Keliling diukur dalam satuan panjang (misalnya, sentimeter, meter), sedangkan luas diukur dalam satuan luas (misalnya, sentimeter persegi, meter persegi). Ini mencerminkan fakta bahwa keliling mengukur jarak, sedangkan luas mengukur area. Dalam aplikasi praktis, kita menggunakan keliling ketika kita berurusan dengan panjang atau jarak di sepanjang tepi lingkaran, sedangkan kita menggunakan luas ketika kita berurusan dengan area yang tertutup oleh lingkaran.
Aplikasi Praktis Perhitungan Keliling Lingkaran
Perhitungan keliling lingkaran memiliki beragam aplikasi dalam kehidupan sehari-hari. Berikut dua contohnya:
- Membangun lintasan lari: Untuk membangun lintasan lari berbentuk lingkaran dengan panjang tertentu, kita perlu menghitung keliling lingkaran yang diinginkan. Misalnya, jika kita ingin lintasan lari sepanjang 400 meter, kita dapat menghitung jari-jari lingkaran yang dibutuhkan menggunakan rumus keliling lingkaran.
- Merancang roda gigi: Dalam mekanika, perhitungan keliling lingkaran penting dalam merancang roda gigi. Keliling roda gigi menentukan jarak yang ditempuh dalam satu putaran, yang memengaruhi rasio kecepatan dan torsi antara roda gigi yang saling terkait.
Aplikasi Praktis Perhitungan Luas Lingkaran
Sama seperti keliling, perhitungan luas lingkaran juga memiliki banyak aplikasi praktis. Berikut dua contohnya:
- Menghitung luas lahan: Jika kita memiliki lahan berbentuk lingkaran, kita dapat menghitung luas lahan tersebut menggunakan rumus luas lingkaran. Informasi ini penting untuk berbagai keperluan, seperti perencanaan tata ruang, perhitungan biaya perawatan, atau penentuan harga jual.
- Menghitung luas kolam renang: Dalam perencanaan pembangunan kolam renang berbentuk lingkaran, perhitungan luas lingkaran dibutuhkan untuk menentukan jumlah air yang dibutuhkan untuk mengisi kolam, serta perhitungan biaya material untuk pembuatannya.
Hubungan Keliling dan Jari-jari Lingkaran
Hubungan antara keliling (K) dan jari-jari (r) lingkaran dapat dinyatakan dalam persamaan berikut:
K = 2πr
di mana π (pi) adalah konstanta matematika yang nilainya sekitar 3.14159.
Keliling Lingkaran dalam Berbagai Satuan: Keliling Lingkaran Yang Memiliki Jari-jari 10 Cm Adalah

Setelah kita memahami perhitungan keliling lingkaran dengan rumus 2πr, mari kita eksplorasi lebih lanjut dengan melihat bagaimana keliling tersebut berubah ketika kita menggunakan satuan pengukuran yang berbeda. Memahami konversi satuan sangat penting dalam berbagai aplikasi, termasuk dalam ilmu ukur dan teknik.
Konversi Keliling Lingkaran
Dengan jari-jari 10 cm, keliling lingkaran dihitung sebagai berikut: Keliling = 2πr = 2
– π
– 10 cm ≈ 62.83 cm. Selanjutnya, kita akan mengkonversi nilai ini ke meter dan kilometer.
Konversi ke meter: Karena 1 meter = 100 cm, maka 62.83 cm dibagi 100 menghasilkan 0.6283 meter.
Konversi ke kilometer: Karena 1 kilometer = 1000 meter, maka 0.6283 meter dibagi 1000 menghasilkan 0.0006283 kilometer.
Pengubahan Satuan Jari-jari
Mengubah satuan jari-jari sebelum menghitung keliling dilakukan dengan cara yang sama seperti konversi satuan panjang lainnya. Misalnya, jika jari-jari diberikan dalam inci, kita perlu mengkonversi inci ke sentimeter (atau satuan lain yang diinginkan) sebelum memasukkannya ke dalam rumus keliling. Satu inci setara dengan sekitar 2.54 sentimeter. Dengan demikian, jari-jari dalam inci harus dikalikan dengan 2.54 untuk mendapatkan nilai dalam sentimeter.
Tabel Keliling Lingkaran
| Satuan | Jari-jari | Keliling (approx.) |
|---|---|---|
| cm | 10 cm | 62.83 cm |
| m | 0.1 m | 0.6283 m |
| km | 0.0001 km | 0.0006283 km |
Pengaruh Perubahan Satuan
Perubahan satuan tidak mengubah nilai keliling lingkaran itu sendiri, hanya representasi numeriknya. Nilai keliling tetap sama, hanya skala pengukuran yang berbeda. Menggunakan satuan yang tepat penting untuk konteks perhitungan dan menghindari kesalahan interpretasi. Sebagai contoh, menyatakan keliling roda sepeda dalam kilometer akan kurang praktis daripada menggunakan sentimeter.
Contoh Keliling Lingkaran dalam Inci
Misalkan jari-jari lingkaran adalah 4 inci. Untuk menghitung kelilingnya dalam sentimeter, kita pertama-tama mengkonversi jari-jari ke sentimeter: 4 inci
– 2.54 cm/inci = 10.16 cm. Kemudian, kita hitung kelilingnya: Keliling = 2πr = 2
– π
– 10.16 cm ≈ 63.69 cm.
Akhir Kata
Kesimpulannya, menghitung keliling lingkaran dengan jari-jari 10 cm merupakan proses yang sederhana namun fundamental dalam pemahaman geometri. Dengan memahami rumus dan langkah-langkah perhitungan, kita dapat menyelesaikan berbagai masalah yang melibatkan lingkaran dan mengaplikasikannya dalam berbagai konteks praktis. Ketepatan dalam memilih nilai π dan pemahaman akan konversi satuan sangat penting untuk mendapatkan hasil yang akurat.






